Implement a stack using singly linked list

Last Updated : 14 Apr, 2023

To implement a stack using the singly linked list concept, all the singly linked list operations should be performed based on Stack operations LIFO(last in first out) and with the help of that knowledge, we are going to implement a stack using a singly linked list.

So we need to follow a simple rule in the implementation of a stack which is last in first out and all the operations can be performed with the help of a top variable. Let us learn how to perform Pop, Push, Peek, and Display operations in the following article:

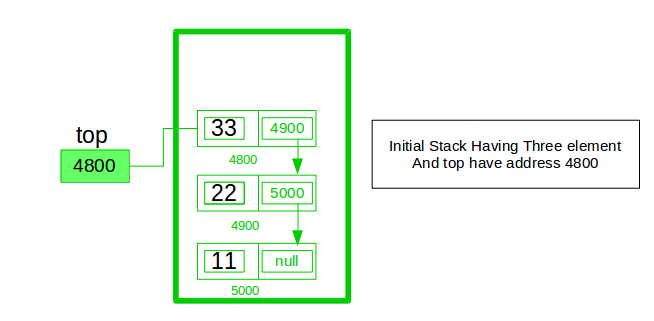
In the stack Implementation, a stack contains a top pointer. which is the “head” of the stack where pushing and popping items happens at the head of the list. The first node has a null in the link field and second node-link has the first node address in the link field and so on and the last node address is in the “top” pointer.

The main advantage of using a linked list over arrays is that it is possible to implement a stack that can shrink or grow as much as needed. Using an array will put a restriction on the maximum capacity of the array which can lead to stack overflow. Here each new node will be dynamically allocated. so overflow is not possible.

Stack Operations:

push(): Insert a new element into the stack i.e just insert a new element at the beginning of the linked list.
pop(): Return the top element of the Stack i.e simply delete the first element from the linked list.
peek(): Return the top element.
display(): Print all elements in Stack.

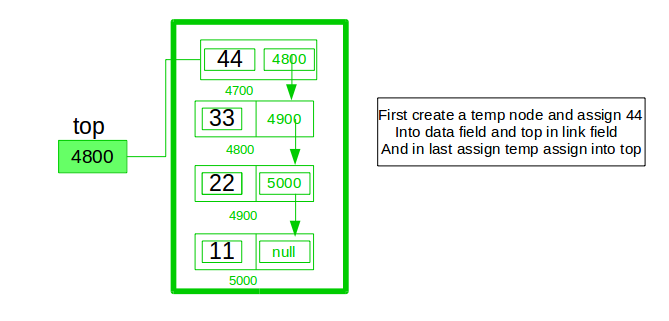
Push Operation:

Initialise a node

Update the value of that node by data i.e. node->data = data

Now link this node to the top of the linked list

And update top pointer to the current node

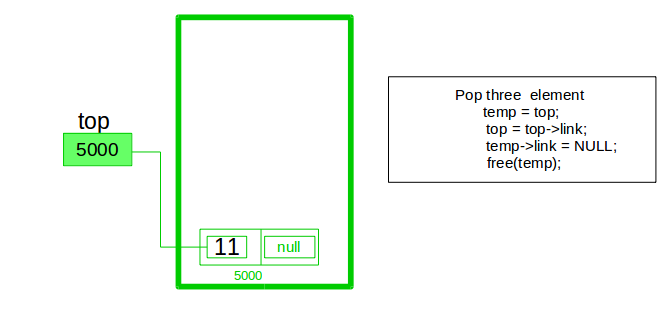
Pop Operation:

First Check whether there is any node present in the linked list or not, if not then return

Otherwise make pointer let say temp to the top node and move forward the top node by 1 step

Now free this temp node

Peek Operation:

Check if there is any node present or not, if not then return.

Otherwise return the value of top node of the linked list

Display Operation:

Take a temp node and initialize it with top pointer

Now start traversing temp till it encounters NULL

Simultaneously print the value of the temp node

Below is the implementation of the above operations

C++

// C++ program to Implement a stack
// using singly linked list
#include <bits/stdc++.h>
using namespace std;
 
// creating a linked list;
class Node {
public:
    int data;
    Node* link;
   
    // Constructor
    Node(int n)
    {
        this->data = n;
        this->link = NULL;
    }
};
 
class Stack {
    Node* top;
 
public:
    Stack() { top = NULL; }
 
    void push(int data)
    {
 
        // Create new node temp and allocate memory in heap
        Node* temp = new Node(data);
 
        // Check if stack (heap) is full.
        // Then inserting an element would
        // lead to stack overflow
        if (!temp) {
            cout << "\nStack Overflow";
            exit(1);
        }
 
        // Initialize data into temp data field
        temp->data = data;
 
        // Put top pointer reference into temp link
        temp->link = top;
 
        // Make temp as top of Stack
        top = temp;
    }
 
    // Utility function to check if
    // the stack is empty or not
    bool isEmpty()
    {
        // If top is NULL it means that
        // there are no elements are in stack
        return top == NULL;
    }
 
    // Utility function to return top element in a stack
    int peek()
    {
        // If stack is not empty , return the top element
        if (!isEmpty())
            return top->data;
        else
            exit(1);
    }
 
    // Function to remove
    // a key from given queue q
    void pop()
    {
        Node* temp;
 
        // Check for stack underflow
        if (top == NULL) {
            cout << "\nStack Underflow" << endl;
            exit(1);
        }
        else {
 
            // Assign top to temp
            temp = top;
 
            // Assign second node to top
            top = top->link;
 
            // This will automatically destroy
            // the link between first node and second node
 
            // Release memory of top node
            // i.e delete the node
            free(temp);
        }
    }
 
    // Function to print all the
    // elements of the stack
    void display()
    {
        Node* temp;
 
        // Check for stack underflow
        if (top == NULL) {
            cout << "\nStack Underflow";
            exit(1);
        }
        else {
            temp = top;
            while (temp != NULL) {
 
                // Print node data
                cout << temp->data;
 
                // Assign temp link to temp
                temp = temp->link;
                if (temp != NULL)
                    cout << " -> ";
            }
        }
    }
};
 
// Driven Program
int main()
{
    // Creating a stack
    Stack s;
 
    // Push the elements of stack
    s.push(11);
    s.push(22);
    s.push(33);
    s.push(44);
 
    // Display stack elements
    s.display();
 
    // Print top element of stack
    cout << "\nTop element is " << s.peek() << endl;
 
    // Delete top elements of stack
    s.pop();
    s.pop();
 
    // Display stack elements
    s.display();
 
    // Print top element of stack
    cout << "\nTop element is " << s.peek() << endl;
 
    return 0;
}

Java

// Java program to Implement a stack
// using singly linked list
// import package
import static java.lang.System.exit;
 
// Driver code
class GFG {
    public static void main(String[] args)
    {
        // create Object of Implementing class
        StackUsingLinkedlist obj
            = new StackUsingLinkedlist();
        // insert Stack value
        obj.push(11);
        obj.push(22);
        obj.push(33);
        obj.push(44);
 
        // print Stack elements
        obj.display();
 
        // print Top element of Stack
        System.out.printf("\nTop element is %d\n",
                          obj.peek());
 
        // Delete top element of Stack
        obj.pop();
        obj.pop();
 
        // print Stack elements
        obj.display();
 
        // print Top element of Stack
        System.out.printf("\nTop element is %d\n",
                          obj.peek());
    }
}
 
// Create Stack Using Linked list
class StackUsingLinkedlist {
 
    // A linked list node
    private class Node {
 
        int data; // integer data
        Node link; // reference variable Node type
    }
    // create global top reference variable global
    Node top;
    // Constructor
    StackUsingLinkedlist() { this.top = null; }
 
    // Utility function to add an element x in the stack
    public void push(int x) // insert at the beginning
    {
        // create new node temp and allocate memory
        Node temp = new Node();
 
        // check if stack (heap) is full. Then inserting an
        //  element would lead to stack overflow
        if (temp == null) {
            System.out.print("\nHeap Overflow");
            return;
        }
 
        // initialize data into temp data field
        temp.data = x;
 
        // put top reference into temp link
        temp.link = top;
 
        // update top reference
        top = temp;
    }
 
    // Utility function to check if the stack is empty or
    // not
    public boolean isEmpty() { return top == null; }
 
    // Utility function to return top element in a stack
    public int peek()
    {
        // check for empty stack
        if (!isEmpty()) {
            return top.data;
        }
        else {
            System.out.println("Stack is empty");
            return -1;
        }
    }
 
    // Utility function to pop top element from the stack
    public void pop() // remove at the beginning
    {
        // check for stack underflow
        if (top == null) {
            System.out.print("\nStack Underflow");
            return;
        }
 
        // update the top pointer to point to the next node
        top = (top).link;
    }
 
    public void display()
    {
        // check for stack underflow
        if (top == null) {
            System.out.printf("\nStack Underflow");
            exit(1);
        }
        else {
            Node temp = top;
            while (temp != null) {
 
                // print node data
                System.out.print(temp.data);
 
                // assign temp link to temp
                temp = temp.link;
                if(temp != null)
                    System.out.print(" -> ");
            }
        }
    }
}

Python3

# python3 program to Implement a stack
# using singly linked list
 
class Node:
 
    # Class to create nodes of linked list
    # constructor initializes node automatically
    def __init__(self, data):
        self.data = data
        self.next = None
 
 
class Stack:
 
    # head is default NULL
    def __init__(self):
        self.head = None
 
    # Checks if stack is empty
    def isempty(self):
        if self.head == None:
            return True
        else:
            return False
 
    # Method to add data to the stack
    # adds to the start of the stack
    def push(self, data):
 
        if self.head == None:
            self.head = Node(data)
 
        else:
            newnode = Node(data)
            newnode.next = self.head
            self.head = newnode
 
    # Remove element that is the current head (start of the stack)
    def pop(self):
 
        if self.isempty():
            return None
 
        else:
            # Removes the head node and makes
            # the preceding one the new head
            poppednode = self.head
            self.head = self.head.next
            poppednode.next = None
            return poppednode.data
 
    # Returns the head node data
    def peek(self):
 
        if self.isempty():
            return None
 
        else:
            return self.head.data
 
    # Prints out the stack
    def display(self):
 
        iternode = self.head
        if self.isempty():
            print("Stack Underflow")
 
        else:
 
            while(iternode != None):
 
                print(iternode.data, end = "")
                iternode = iternode.next
                if(iternode != None):
                    print(" -> ", end = "")
            return
 
 
# Driver code
if __name__ == "__main__":
  MyStack = Stack()
   
  MyStack.push(11)
  MyStack.push(22)
  MyStack.push(33)
  MyStack.push(44)
 
  # Display stack elements
  MyStack.display()
 
  # Print top element of stack
  print("\nTop element is ", MyStack.peek())
 
  # Delete top elements of stack
  MyStack.pop()
  MyStack.pop()
 
  # Display stack elements
  MyStack.display()
 
  # Print top element of stack
  print("\nTop element is ", MyStack.peek())
 
# This code is contributed by Mathew George

C#

// C# program to Implement a stack
// using singly linked list
 
// import package
using System;
 
// Create Stack Using Linked list
public class StackUsingLinkedlist {
 
    // A linked list node
    private class Node {
        // integer data
        public int data;
 
        // reference variable Node type
        public Node link;
    }
 
    // create global top reference variable
    Node top;
 
    // Constructor
    public StackUsingLinkedlist() { this.top = null; }
 
    // Utility function to add
    // an element x in the stack
    // insert at the beginning
    public void push(int x)
    {
        // create new node temp and allocate memory
        Node temp = new Node();
 
        // check if stack (heap) is full.
        // Then inserting an element
        // would lead to stack overflow
        if (temp == null) {
            Console.Write("\nHeap Overflow");
            return;
        }
 
        // initialize data into temp data field
        temp.data = x;
 
        // put top reference into temp link
        temp.link = top;
 
        // update top reference
        top = temp;
    }
 
    // Utility function to check if
    // the stack is empty or not
    public bool isEmpty() { return top == null; }
 
    // Utility function to return
    // top element in a stack
    public int peek()
    {
        // check for empty stack
        if (!isEmpty()) {
            return top.data;
        }
        else {
            Console.WriteLine("Stack is empty");
            return -1;
        }
    }
 
    // Utility function to pop top element from the stack
    public void pop() // remove at the beginning
    {
        // check for stack underflow
        if (top == null) {
            Console.Write("\nStack Underflow");
            return;
        }
 
        // update the top pointer to
        // point to the next node
        top = (top).link;
    }
 
    public void display()
    {
        // check for stack underflow
        if (top == null) {
            Console.Write("\nStack Underflow");
            return;
        }
        else {
            Node temp = top;
            while (temp != null) {
 
                // print node data
                Console.Write(temp.data);
 
                // assign temp link to temp
                temp = temp.link;
                if(temp != null)
                    Console.Write(" -> ");
            }
        }
    }
}
 
// Driver code
public class GFG {
    public static void Main(String[] args)
    {
        // create Object of Implementing class
        StackUsingLinkedlist obj
            = new StackUsingLinkedlist();
 
        // insert Stack value
        obj.push(11);
        obj.push(22);
        obj.push(33);
        obj.push(44);
 
        // print Stack elements
        obj.display();
 
        // print Top element of Stack
        Console.Write("\nTop element is {0}\n", obj.peek());
 
        // Delete top element of Stack
        obj.pop();
        obj.pop();
 
        // print Stack elements
        obj.display();
 
        // print Top element of Stack
        Console.Write("\nTop element is {0}\n", obj.peek());
    }
}
 
// This code is contributed by 29AjayKumar

Javascript

// Javascript program to Implement a stack
// using singly linked list
// import package
 
// A linked list node
class Node
{
    constructor()
    {
        this.data=0;
        this.link=null;
    }
}
 
// Create Stack Using Linked list
class StackUsingLinkedlist
{
    constructor()
    {
        this.top=null;
    }
     
    // Utility function to add an element x in the stack
    push(x)
    {
        // create new node temp and allocate memory
        let temp = new Node();
  
        // check if stack (heap) is full. Then inserting an
        //  element would lead to stack overflow
        if (temp == null) {
            document.write("<br>Heap Overflow");
            return;
        }
  
        // initialize data into temp data field
        temp.data = x;
  
        // put top reference into temp link
        temp.link = this.top;
  
        // update top reference
        this.top = temp;
    }
     
     // Utility function to check if the stack is empty or not
    isEmpty()
    {
         return this.top == null;
    }
     
    // Utility function to return top element in a stack    
    peek()
    {
        // check for empty stack
        if (!this.isEmpty()) {
            return this.top.data;
        }
        else {
            document.write("Stack is empty<br>");
            return -1;
        }
    }
     
    // Utility function to pop top element from the stack
    pop() // remove at the beginning
    {
        // check for stack underflow
        if (this.top == null) {
            document.write("<br>Stack Underflow");
            return;
        }
  
        // update the top pointer to point to the next node
        this.top = this.top.link;
    }
     
    display()
    {
        // check for stack underflow
        if (this.top == null) {
            document.write("<br>Stack Underflow");
             
        }
        else {
            let temp = this.top;
            while (temp != null) {
  
                // print node data
                document.write(temp.data+"->");
  
                // assign temp link to temp
                temp = temp.link;
            }
        }
    }
}
 
// main class
 
// create Object of Implementing class
let obj = new StackUsingLinkedlist();
// insert Stack value
obj.push(11);
obj.push(22);
obj.push(33);
obj.push(44);
 
// print Stack elements
obj.display();
 
// print Top element of Stack
document.write("<br>Top element is ", obj.peek()+"<br>");
 
// Delete top element of Stack
obj.pop();
obj.pop();
 
// print Stack elements
obj.display();
 
// print Top element of Stack
document.write("<br>Top element is ", obj.peek()+"<br>");
 
// This code is contributed by rag2127

Output

44 -> 33 -> 22 -> 11
Top element is 44
22 -> 11
Top element is 22

Time Complexity: O(1), for all push(), pop(), and peek(), as we are not performing any kind of traversal over the list. We perform all the operations through the current pointer only.
Auxiliary Space: O(N), where N is the size of the stack

In this implementation, we define a Node class that represents a node in the linked list, and a Stack class that uses this node class to implement the stack. The head attribute of the Stack class points to the top of the stack (i.e., the first node in the linked list).

To push an item onto the stack, we create a new node with the given item and set its next pointer to the current head of the stack. We then set the head of the stack to the new node, effectively making it the new top of the stack.

To pop an item from the stack, we simply remove the first node from the linked list by setting the head of the stack to the next node in the list (i.e., the node pointed to by the next pointer of the current head). We return the data stored in the original head node, which is the item that was removed from the top of the stack.

Benefits of implementing a stack using a singly linked list include:

Dynamic memory allocation: The size of the stack can be increased or decreased dynamically by adding or removing nodes from the linked list, without the need to allocate a fixed amount of memory for the stack upfront.

Efficient memory usage: Since nodes in a singly linked list only have a next pointer and not a prev pointer, they use less memory than nodes in a doubly linked list.

Easy implementation: Implementing a stack using a singly linked list is straightforward and can be done using just a few lines of code.

Versatile: Singly linked lists can be used to implement other data structures such as queues, linked lists, and trees.

In summary, implementing a stack using a singly linked list is a simple and efficient way to create a dynamic stack data structure in Python.

Real time examples of stack:

Stacks are used in various real-world scenarios where a last-in, first-out (LIFO) data structure is required. Here are some examples of real-time applications of stacks:

Function call stack: When a function is called in a program, the return address and all the function parameters are pushed onto the function call stack. The stack allows the function to execute and return to the caller function in the reverse order in which they were called.

Undo/Redo operations: In many applications, such as text editors, image editors, or web browsers, the undo and redo functionalities are implemented using a stack. Every time an action is performed, it is pushed onto the stack. When the user wants to undo the last action, the top element of the stack is popped and the action is reversed.

Browser history: Web browsers use stacks to keep track of the pages visited by the user. Every time a new page is visited, its URL is pushed onto the stack. When the user clicks the “Back” button, the last visited URL is popped from the stack and the user is directed to the previous page.

Expression evaluation: Stacks are used in compilers and interpreters to evaluate expressions. When an expression is parsed, it is converted into postfix notation and pushed onto a stack. The postfix expression is then evaluated using the stack.

Call stack in recursion: When a recursive function is called, its call is pushed onto the stack. The function executes and calls itself, and each subsequent call is pushed onto the stack. When the recursion ends, the stack is popped, and the program returns to the previous function call.

In summary, stacks are widely used in many applications where LIFO functionality is required, such as function calls, undo/redo operations, browser history, expression evaluation, and recursive function calls.

Suggest improvement

Applications, Advantages and Disadvantages of Stack

Introduction to Monotonic Stack - Data Structure and Algorithm Tutorials

Share your thoughts in the comments

Stack implementation in different language

Some questions related to Stack implementation

Easy problems on Stack

Intermediate problems on Stack

Hard problems on Stack