Stack for Competitive Programming

Last Updated : 09 Jan, 2024

For competitive programming to be successful, efficient data structures and algorithms are essential. The stack is one such tool. In this article, we will examine how stack data structures play an important role in solving problems efficiently during competitive programming challenges. We will explore the basics of stacks with its use cases and some important problems related to stack that will help you to sharpen your competitive programming skills.

Table of Content

Introduction of Stack
Stack Operations
Must do Stack problems to understand the working of Stack
Use Cases of Stack in Competitive Programming
Practice problems on Stack for Competitive Programming

Introduction of Stack

A stack is a linear data structure in which the insertion of a new element and removal of an existing element takes place at the same end represented as the top of the stack. A Stack works on the LIFO process (Last In First Out), i.e., the element that was inserted last will be removed first.

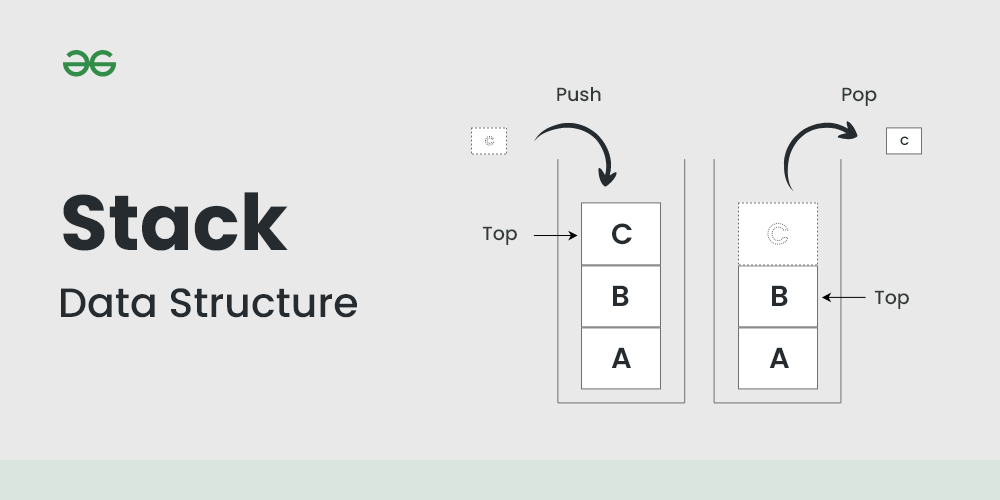
Stack Data Structure

Declaring a Stack

C++

#include<iostream>
#include <stack>
using namespace std;
int main(){
  stack<dataType> myStack;
}

Java

import java.util.Stack;
 
public class Main {
    public static void main(String[] args) {
        Stack<DataType> myStack = new Stack<>();
    }
}

Python3

my_stack = []

C#

using System;
using System.Collections.Generic;
 
public class Main
{
    public static void Main(string[] args)
    {
        Stack<DataType> myStack = new Stack<DataType>();
    }
 
    // Define DataType class if not already defined
    public class DataType
    {
        // Define class members if necessary
    }
}

Javascript

let myStack = [];

Stack Operations

There are various stack operations that are applicable on a stack. Stack operations are generally used to extract information and data from a stack data structure.

Some of the stack operations are given below:

1. Push element X into the stack

C++

myStack.push(X);

Java

myStack.push(X);

Python3

myStack.push(X);

C#

myStack.Push(X);

Javascript

myStack.push(X);

2. Pop the topmost element of the stack

C++

myStack.pop();

Java

myStack.pop();

Python3

myStack.pop()

C#

myStack.Pop();

Javascript

myStack.pop();

3. Get the Topmost of the stack

C++

int topElement = myStack.top();

Java

int topElement = myStack.top();

Python3

top_element = my_stack[-1]

C#

int topElement = myStack.Top();

Javascript

let topElement = myStack[myStack.length - 1];

4. Size of Stack

C++

int stackSize = myStack.size();

Java

int stackSize = myStack.size();

Python3

stack_size = len(my_stack)

C#

int stackSize = myStack.Size();

Javascript

let stackSize = myStack.length;

5. Checks if the stack is empty

C++

if (myStack.empty()) {
    // Stack is empty
}

Java

if (myStack.isEmpty()) {
    // Stack is empty
}

Python3

if not my_stack:
    # Stack is empty

C#

if (myStack.Empty()) {
    // Stack is empty
}

Javascript

if (myStack.length === 0) {
    // Stack is empty
}

6. Swap two stacks

C++

stack<int> myStack;
stack<int> anotherStack;
myStack.swap(anotherStack);

Java

// Using Deque instead of Stack for flexibility
Deque<Integer> myStack = new ArrayDeque<>();
Deque<Integer> anotherStack = new ArrayDeque<>();
 
// Add elements to myStack and anotherStack
 
// Swap the contents of myStack and anotherStack using a
// temporary variable
Deque<Integer> tempStack = myStack;
myStack = anotherStack;
anotherStack = tempStack;

Python3

my_stack = []
another_stack = []
 
# Add elements to my_stack and another_stack
 
# Swap the contents of my_stack and another_stack
my_stack, another_stack = another_stack, my_stack

C#

// Using Queue instead of Stack for flexibility
Queue<int> myStack = new Queue<int>();
Queue<int> anotherStack = new Queue<int>();
 
// Add elements to myStack and anotherStack
 
// Swap the contents of myStack and anotherStack using a temporary variable
Queue<int> tempStack = myStack;
myStack = anotherStack;
anotherStack = tempStack;

Javascript

let myStack = []; 
let anotherStack = [];
 
// Add elements to myStack and anotherStack
 
// Swap the contents of myStack and anotherStack using array destructuring
[myStack, anotherStack] = [anotherStack, myStack];

Must do Stack problems to understand the working of Stack

Problem	Practice link
Convert Infix expression to Postfix expression	Solve
Evaluation of Postfix Expression	Solve
Check for Balanced Brackets in an expression	Solve
Implement Stack using Queues	Solve

Use Cases of Stack in Competitive Programming

Here are some use cases of the stack data structure in competitive programming:

1. Next Greater element in O(N) / Next Smaller Element in O(N)

Many coding problems requires the pre-calculation of next smaller/greater element for each index of the array on left as well as right side. This can be calculated using stack in O(N) complexity

Example: Arr = [4,2,1,5,2,3,1]
Next greater on Left: [-1,4,2,-1,5,5,3] //-1 indicates that no greater element exists on left
Next greater on right:[5,5,5,-1,3,-1,-1] //-1 indicates that no greater element exists on right
Next smaller on left: [-1,-1,-1,1,1,2,-1] //-1 indicates that no smaller element exists on left
Next smaller on right:[2,1,-1,2,1,1,-1] //-1 indicates that no smaller element exists on right

2. Balanced Bracket Problems

Bracket problems in programming typically refer to problems that involve working with parentheses, and/or braces in expressions or sequences. It typically refers to problems related to the correct and balanced usage of parentheses, and braces in expressions or code.

These problems often involve checking if a given sequence of these symbols is well-formed, meaning that each opening symbol has a corresponding closing symbol in the correct order, and there are no unmatched or incorrectly nested symbols.

The most basic problem that falls under this category is balanced parenthesis, which state that Given a string containing various types of parentheses, such as ‘(‘, ‘)’, ‘{‘, ‘}’, ‘[‘, ‘]’, you need to determine if the parentheses are balanced.

This problem is solved using a stack data structure. A stack can help you keep track of the opening parentheses you’ve seen so far. When you encounter a closing parenthesis, you can easily check if the top element of the stack matches it. If it does, you pop the opening parenthesis from the stack, indicating that it has been properly closed.

3. Monotonic Stacks

A monotonic stack is a stack whose elements are monotonically increasing or decreasing. It contains all qualities that a typical stack has and its elements are all monotonic decreasing or increasing.

Below are the features of a monotonic stack:

It is a range of queries in an array situation
The minima/maxima elements
When an element is popped from the monotonic stack, it will never be utilised again.

The monotonic stack problem is mainly the previous/next smaller/larger problem. It maintains monotonicity while popping elements when a new item is pushed into the stack.

4. Find the minimum in all subarrays of a fixed length in an array in O(N)

Suppose we have a problem in which we need to calculate the maximum for each and every contiguous subarray of size K for a given any given array. This problem can be solved in O(n) using a Deque data structure which has functionality of a stack as well as a queue. click here to see how.

5. Finding Cycle in a directed graph

To find cycle in a directed graph we can use the Depth First Traversal (DFS) technique. It is based on the idea that there is a cycle in a graph only if there is a back edge [i.e., a node points to one of its ancestors] present in the graph.

To detect a back edge, we need to keep track of the nodes visited till now and the nodes that are in the current recursion stack [i.e., the current path that we are visiting]. If during recursion, we reach a node that is already in the recursion stack, there is a cycle present in the graph.

Practice problems on Stack for Competitive Programming

Problem	Practice link
Largest Rectangular Area in a Histogram using Stack	Solve
Merge Overlapping Intervals	Solve
Design a stack that supports getMin() in O(1) time and O(1) extra space	Solve
Maximum size rectangle binary sub-matrix with all 1s	Solve
The Stock Span Problem	Solve
The Celebrity Problem	Solve
ZigZag Tree Traversal	Solve
Length of the longest valid substring	Solve
Reduce the string by removing K consecutive identical characters	Solve
Minimum number of bracket reversals needed to make an expression balanced	Solve

Suggest improvement

Remove all redundant parenthesis

Number of subarray's of K size with Even Bitwise-OR

Share your thoughts in the comments

Stack for Competitive Programming

Introduction of Stack

Declaring a Stack

C++

Java

Python3

C#

Javascript

Stack Operations

1. Push element X into the stack

C++

Java

Python3

C#

Javascript

2. Pop the topmost element of the stack

C++

Java

Python3

C#

Javascript

3. Get the Topmost of the stack

C++

Java

Python3

C#

Javascript

4. Size of Stack

C++

Java

Python3

C#

Javascript

5. Checks if the stack is empty

C++

Java

Python3

C#

Javascript

6. Swap two stacks

C++

Java

Python3

C#

Javascript

Must do Stack problems to understand the working of Stack

Use Cases of Stack in Competitive Programming

1. Next Greater element in O(N) / Next Smaller Element in O(N)

2. Balanced Bracket Problems

3. Monotonic Stacks

4. Find the minimum in all subarrays of a fixed length in an array in O(N)

5. Finding Cycle in a directed graph

Practice problems on Stack for Competitive Programming

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?