Find a triplet such that sum of two equals to third element

Last Updated : 19 Sep, 2023

Given an array of integers, you have to find three numbers such that the sum of two elements equals the third element.

Examples:

Input : {5, 32, 1, 7, 10, 50, 19, 21, 2}
Output : 21, 2, 19

Input : {5, 32, 1, 7, 10, 50, 19, 21, 0}
Output : no such triplet exist

Question source: Arcesium Interview Experience | Set 7 (On campus for Internship)

Simple approach: Run three loops and check if there exists a triplet such that sum of two elements equals the third element.

Code-

C++

// CPP program to find three numbers 
// such that sum of two makes the 
// third element in array 
#include <bits/stdc++.h> 
using namespace std; 
  
// Utility function for finding 
// triplet in array 
void findTriplet(int arr[], int n) 
{   
     for (int i = 0; i < n; i++) { 
        for (int j = i + 1; j < n; j++) { 
          for(int k = j + 1; k < n; k++) { 
                 if((arr[i]+arr[j]==arr[k]) || (arr[i]+arr[k]==arr[j]) || (arr[j]+arr[k]==arr[i])){ 
                     // printing out the first triplet 
                      cout << "Numbers are: " << arr[i] << " "
                     << arr[j] << " " << arr[k]; 
                    return;  
                 } 
                 
            } 
        } 
    } 
  
    // No such triplet is found in array 
    cout << "No such triplet exists"; 
} 
  
// driver program 
int main() 
{ 
    int arr[] = { 5, 32, 1, 7, 10, 50, 19, 21, 2 }; 
    int n = sizeof(arr) / sizeof(arr[0]); 
  
    findTriplet(arr, n); 
    return 0; 
} 

Java

import java.util.*; 
  
public class Main { 
  
  // Utility function for finding triplet in array 
  public static void findTriplet(int[] arr, int n) { 
    for (int i = 0; i < n; i++) { 
      for (int j = i + 1; j < n; j++) { 
        for(int k = j + 1; k < n; k++) { 
          if((arr[i]+arr[j]==arr[k]) || (arr[i]+arr[k]==arr[j]) || (arr[j]+arr[k]==arr[i])) { 
  
            // printing out the first triplet 
            System.out.println("Numbers are: " + arr[i] + " " + arr[j] + " " + arr[k]); 
            return; 
          } 
        } 
      } 
    } 
    // No such triplet is found in array 
    System.out.println("No such triplet exists"); 
  } 
  
  // Driver program 
  public static void main(String[] args) { 
    int[] arr = { 5, 32, 1, 7, 10, 50, 19, 21, 2 }; 
    int n = arr.length; 
  
    findTriplet(arr, n); 
  } 
} 

Python3

# Python3 program to find three numbers 
# such that sum of two makes the 
# third element in array 
  
# Utility function for finding 
# triplet in array 
def findTriplet(arr, n): 
    for i in range(n): 
        for j in range(i + 1, n): 
            for k in range(j + 1, n): 
                if((arr[i]+arr[j] == arr[k]) or (arr[i]+arr[k] == arr[j]) or (arr[j]+arr[k] == arr[i])): 
                    # printing out the first triplet 
                    print("Numbers are:", arr[i], arr[j], arr[k]) 
                    return
  
    # No such triplet is found in array 
    print("No such triplet exists") 
  
  
# driver program 
if __name__ == '__main__': 
    arr = [5, 32, 1, 7, 10, 50, 19, 21, 2] 
    n = len(arr) 
  
    findTriplet(arr, n) 

C#

// C# program to find three numbers 
// such that sum of two makes the 
// third element in array 
using System; 
  
public class MainClass { 
    // Utility function for finding 
    // triplet in array 
    public static void FindTriplet(int[] arr, int n) 
    { 
        for (int i = 0; i < n; i++) { 
            for (int j = i + 1; j < n; j++) { 
                for (int k = j + 1; k < n; k++) { 
                    if ((arr[i] + arr[j] == arr[k]) 
                        || (arr[i] + arr[k] == arr[j]) 
                        || (arr[j] + arr[k] == arr[i])) { 
                        // printing out the first triplet 
                        Console.WriteLine( 
                            "Numbers are: " + arr[i] + " "
                            + arr[j] + " " + arr[k]); 
                        return; 
                    } 
                } 
            } 
        } 
  
        // No such triplet is found in array 
        Console.WriteLine("No such triplet exists"); 
    } 
  
    public static void Main() 
    { 
        int[] arr = { 5, 32, 1, 7, 10, 50, 19, 21, 2 }; 
        int n = arr.Length; 
  
        FindTriplet(arr, n); 
    } 
}

Javascript

// Utility function for finding triplet in array 
function findTriplet(arr) { 
  const n = arr.length; 
  
  for (let i = 0; i < n; i++) { 
    for (let j = i + 1; j < n; j++) { 
      for (let k = j + 1; k < n; k++) { 
        if ( 
          arr[i] + arr[j] === arr[k] || 
          arr[i] + arr[k] === arr[j] || 
          arr[j] + arr[k] === arr[i] 
        ) { 
          // Printing out the first triplet 
          console.log(`Numbers are: ${arr[i]}, ${arr[j]}, ${arr[k]}`); 
          return; 
        } 
      } 
    } 
  } 
  
  // No such triplet is found in array 
  console.log("No such triplet exists"); 
} 
  
// Driver program 
const arr = [5, 32, 1, 7, 10, 50, 19, 21, 2]; 
findTriplet(arr); 

Output

Numbers are: 5 7 2

Time Complexity: O(N^3)
Auxiliary Space: O(1)

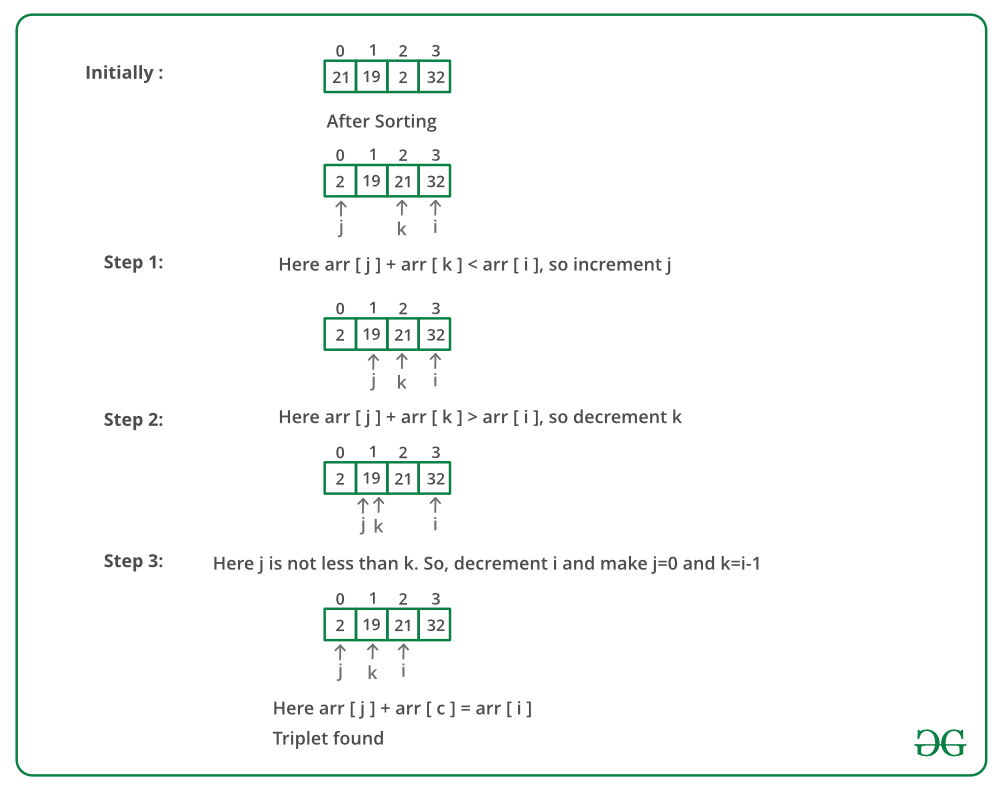
Efficient approach: The idea is similar to Find a triplet that sum to a given value.

Sort the given array first.
Start fixing the greatest element of three from the back and traverse the array to find the other two numbers which sum up to the third element.
Take two pointers j(from front) and k(initially i-1) to find the smallest of the two number and from i-1 to find the largest of the two remaining numbers
If the addition of both the numbers is still less than A[i], then we need to increase the value of the summation of two numbers, thereby increasing the j pointer, so as to increase the value of A[j] + A[k].
If the addition of both the numbers is more than A[i], then we need to decrease the value of the summation of two numbers, thereby decrease the k pointer so as to decrease the overall value of A[j] + A[k].

Below image is a dry run of the above approach:

Below is the implementation of the above approach:

C++

// CPP program to find three numbers 
// such that sum of two makes the 
// third element in array 
#include <bits/stdc++.h> 
using namespace std; 
  
// Utility function for finding 
// triplet in array 
void findTriplet(int arr[], int n) 
{ 
    // sort the array 
    sort(arr, arr + n); 
  
    // for every element in arr 
    // check if a pair exist(in array) whose 
    // sum is equal to arr element 
    for (int i = n - 1; i >= 0; i--) { 
        int j = 0; 
        int k = i - 1; 
  
        // Iterate forward and backward to find 
        // the other two elements 
        while (j < k) { 
  
            // If the two elements sum is 
            // equal to the third element 
            if (arr[i] == arr[j] + arr[k]) { 
  
                // pair found 
                cout << "numbers are " << arr[i] << " "
                     << arr[j] << " " << arr[k] << endl; 
                return; 
            } 
  
            // If the element is greater than 
            // sum of both the elements, then try 
            // adding a smaller number to reach the 
            // equality 
            else if (arr[i] > arr[j] + arr[k]) 
                j += 1; 
  
            // If the element is smaller, then 
            // try with a smaller number 
            // to reach equality, so decrease K 
            else
                k -= 1; 
        } 
    } 
  
    // No such triplet is found in array 
    cout << "No such triplet exists"; 
} 
  
// driver program 
int main() 
{ 
    int arr[] = { 5, 32, 1, 7, 10, 50, 19, 21, 2 }; 
    int n = sizeof(arr) / sizeof(arr[0]); 
  
    findTriplet(arr, n); 
    return 0; 
} 

Java

// Java program to find three numbers 
// such that sum of two makes the 
// third element in array 
import java.util.Arrays; 
  
public class GFG { 
  
    // utility function for finding 
    // triplet in array 
    static void findTriplet(int arr[], int n) 
    { 
        // sort the array 
        Arrays.sort(arr); 
  
        // for every element in arr 
        // check if a pair exist(in array) whose 
        // sum is equal to arr element 
        for (int i = n - 1; i >= 0; i--) { 
            int j = 0; 
            int k = i - 1; 
            while (j < k) { 
                if (arr[i] == arr[j] + arr[k]) { 
  
                    // pair found 
                    System.out.println("numbers are " + arr[i] + " "
                                       + arr[j] + " " + arr[k]); 
  
                    return; 
                } 
                else if (arr[i] > arr[j] + arr[k]) 
                    j += 1; 
                else
                    k -= 1; 
            } 
        } 
  
        // no such triplet is found in array 
        System.out.println("No such triplet exists"); 
    } 
  
    // driver program 
    public static void main(String args[]) 
    { 
        int arr[] = { 5, 32, 1, 7, 10, 50, 19, 21, 2 }; 
        int n = arr.length; 
        findTriplet(arr, n); 
    } 
} 
// This code is contributed by Sumit Ghosh 

Python

# Python program to find three numbers 
# such that sum of two makes the 
# third element in array 
  
# utility function for finding 
# triplet in array 
def findTriplet(arr, n): 
      
    # sort the array 
    arr.sort() 
   
    # for every element in arr 
    # check if a pair exist(in array) whose 
    # sum is equal to arr element 
    i = n - 1
    while(i >= 0): 
        j = 0
        k = i - 1
        while (j < k): 
            if (arr[i] == arr[j] + arr[k]): 
                 
                # pair found 
                print "numbers are ", arr[i], arr[j], arr[k] 
                return
            elif (arr[i] > arr[j] + arr[k]): 
                j += 1
            else: 
                k -= 1
        i -= 1
          
    # no such triplet is found in array 
    print "No such triplet exists"
   
# driver program 
arr = [ 5, 32, 1, 7, 10, 50, 19, 21, 2 ] 
n = len(arr) 
findTriplet(arr, n) 
  
# This code is contributed by Sachin Bisht 

C#

// C# program to find three numbers 
// such that sum of two makes the 
// third element in array 
using System; 
  
public class GFG { 
  
    // utility function for finding 
    // triplet in array 
    static void findTriplet(int[] arr, int n) 
    { 
  
        // sort the array 
        Array.Sort(arr); 
  
        // for every element in arr 
        // check if a pair exist(in 
        // array) whose sum is equal 
        // to arr element 
        for (int i = n - 1; i >= 0; i--) { 
            int j = 0; 
            int k = i - 1; 
            while (j < k) { 
                if (arr[i] == arr[j] + arr[k]) { 
  
                    // pair found 
                    Console.WriteLine("numbers are "
                                      + arr[i] + " " + arr[j] 
                                      + " " + arr[k]); 
  
                    return; 
                } 
                else if (arr[i] > arr[j] + arr[k]) 
                    j += 1; 
                else
                    k -= 1; 
            } 
        } 
  
        // no such triplet is found in array 
        Console.WriteLine("No such triplet exists"); 
    } 
  
    // driver program 
    public static void Main() 
    { 
        int[] arr = { 5, 32, 1, 7, 10, 50, 
                      19, 21, 2 }; 
        int n = arr.Length; 
  
        findTriplet(arr, n); 
    } 
} 
  
// This code is contributed by vt_m. 

PHP

<?php 
// PHP program to find three 
// numbers such that sum of  
// two makes the third 
// element in array 
  
// utility function for  
// finding triplet in array 
function findTriplet($arr, $n) 
{ 
    // sort the array 
    sort($arr); 
  
    // for every element in  
    // arr check if a pair  
    // exist(in array) whose 
    // sum is equal to arr element 
    for ($i = $n - 1; $i >= 0; $i--) 
    { 
        $j = 0; 
        $k = $i - 1; 
        while ($j < $k)  
        { 
            if ($arr[$i] == $arr[$j] + $arr[$k])  
            { 
                  
                // pair found 
                echo "numbers are ", $arr[$i], " ",  
                                      $arr[$j], " ",  
                                      $arr[$k]; 
                return; 
            }  
            else if ($arr[$i] > $arr[$j] +  
                                $arr[$k]) 
                $j += 1; 
            else
                $k -= 1; 
        } 
    } 
  
    // no such triplet  
    // is found in array 
    echo "No such triplet exists"; 
} 
  
// Driver Code 
$arr = array(5, 32, 1, 7, 10,  
             50, 19, 21, 2 ); 
$n = count($arr); 
  
findTriplet($arr, $n); 
  
// This code is contributed by anuj_67. 
?> 

Javascript

<script> 
  
// Javascript program to find three numbers 
// such that sum of two makes the 
// third element in array 
  
  
// Utility function for finding 
// triplet in array 
function findTriplet(arr, n) 
{ 
    // sort the array 
    arr.sort((a,b) => a-b); 
  
    // for every element in arr 
    // check if a pair exist(in array) whose 
    // sum is equal to arr element 
    for (let i = n - 1; i >= 0; i--) { 
        let j = 0; 
        let k = i - 1; 
  
        // Iterate forward and backward to find 
        // the other two elements 
        while (j < k) { 
  
            // If the two elements sum is 
            // equal to the third element 
            if (arr[i] == arr[j] + arr[k]) { 
  
                // pair found 
                document.write("numbers are " + arr[i] + 
                " " + arr[j] + " " + arr[k] + "<br>"); 
                return; 
            } 
  
            // If the element is greater than 
            // sum of both the elements, then try 
            // adding a smaller number to reach the 
            // equality 
            else if (arr[i] > arr[j] + arr[k]) 
                j += 1; 
  
            // If the element is smaller, then 
            // try with a smaller number 
            // to reach equality, so decrease K 
            else
                k -= 1; 
        } 
    } 
  
    // No such triplet is found in array 
    document.write("No such triplet exists"); 
} 
  
// driver program 
  
    let arr = [ 5, 32, 1, 7, 10, 50, 19, 21, 2 ]; 
    let n = arr.length; 
  
    findTriplet(arr, n); 
  
// This code is contributed by Mayank Tyagi 
  
</script> 

Output

numbers are 21 2 19

Time Complexity: O(N^2)
Auxiliary Space: O(1)

Another Approach: The idea is similar to previous approach:

Sort the given array.
Start a nested loop, fixing the first element i(from 0 to n-1) and moving the other one j (from i+1 to n-1).
Take the sum of both the elements and search it in the remaining array using Binary Search.

Implementation:

C++

// CPP program to find three numbers 
// such that sum of two makes the 
// third element in array 
#include <bits/stdc++.h> 
#include <iostream> 
using namespace std; 
  
// function to perform binary search 
bool search(int sum, int start, int end, int arr[]) 
{ 
    while (start <= end) { 
        int mid = (start + end) / 2; 
        if (arr[mid] == sum) { 
            return true; 
        } 
        else if (arr[mid] > sum) { 
            end = mid - 1; 
        } 
        else { 
            start = mid + 1; 
        } 
    } 
    return false; 
} 
  
// function to find the triplets 
void findTriplet(int arr[], int n) 
{ 
    // sorting the array 
    sort(arr, arr + n); 
  
    // initialising nested loops 
    for (int i = 0; i < n; i++) { 
        for (int j = i + 1; j < n; j++) { 
  
            // finding the sum of the numbers 
            if (search((arr[i] + arr[j]), j, n - 1, arr)) { 
  
                // printing out the first triplet 
                cout << "Numbers are: " << arr[i] << " "
                     << arr[j] << " " << (arr[i] + arr[j]); 
                return; 
            } 
        } 
    } 
    // if no such triplets are found 
    cout << "No such numbers exist" << endl; 
} 
  
int main() 
{ 
    int arr[] = { 5, 32, 1, 7, 10, 50, 19, 21, 2 }; 
    int n = sizeof(arr) / sizeof(arr[0]); 
    findTriplet(arr, n); 
    return 0; 
} 
  
// This code is contributed by Sarthak Delori

Java

// Java program to find three numbers 
// such that sum of two makes the 
// third element in array 
import java.util.*; 
  
class GFG{ 
  
// Function to perform binary search 
static boolean search(int sum, int start,  
                      int end, int arr[]) 
{ 
    while (start <= end)  
    { 
        int mid = (start + end) / 2; 
        if (arr[mid] == sum)  
        { 
            return true; 
        } 
        else if (arr[mid] > sum) 
        { 
            end = mid - 1; 
        } 
        else
        { 
            start = mid + 1; 
        } 
    } 
    return false; 
} 
  
// Function to find the triplets 
static void findTriplet(int arr[], int n) 
{ 
      
    // Sorting the array 
    Arrays.sort(arr); 
  
    // Initialising nested loops 
    for(int i = 0; i < n; i++)  
    { 
        for(int j = i + 1; j < n; j++)  
        { 
              
            // Finding the sum of the numbers 
            if (search((arr[i] + arr[j]), j, n - 1, arr))  
            { 
                  
                // Printing out the first triplet 
                System.out.print("Numbers are: " + arr[i] + " " +  
                                   arr[j] + " " + (arr[i] + arr[j])); 
                return; 
            } 
        } 
    } 
      
    // If no such triplets are found 
    System.out.print("No such numbers exist"); 
} 
  
// Driver code 
public static void main(String args[]) 
{ 
    int arr[] = { 5, 32, 1, 7, 10, 50, 19, 21, 2 }; 
    int n = arr.length; 
      
    findTriplet(arr, n); 
} 
} 
  
// This code is contributed by target_2

Python3

# Python program to find three numbers 
# such that sum of two makes the 
# third element in array 
from functools import cmp_to_key 
  
def mycmp(a, b): 
    return a - b  
  
def search(sum, start, end, arr): 
  
    while (start <= end): 
        mid = (start + end) // 2
        if (arr[mid] == sum): 
            return True
        elif (arr[mid] > sum): 
            end = mid - 1
        else: 
            start = mid + 1
  
    return False
  
# Utility function for finding 
# triplet in array 
def findTriplet(arr, n): 
  
    # sort the array 
    arr.sort(key = cmp_to_key(mycmp)) 
  
    # initialising nested loops 
    for i in range(n): 
        for j in range(i + 1,n): 
            if (search((arr[i] + arr[j]), j, n - 1, arr)): 
                print(f"numbers are {arr[i]} {arr[j]} {( arr[i] + arr[j] )}") 
                return
  
    # No such triplet is found in array 
    print("No such triplet exists") 
  
# driver program 
arr = [ 5, 32, 1, 7, 10, 50, 19, 21, 2 ] 
n = len(arr) 
  
findTriplet(arr, n) 
  
# This code is contributed by shinjanpatra

C#

// C# program to find three numbers 
// such that sum of two makes the 
// third element in array 
using System; 
public class GFG { 
  
  // function to perform binary search 
  static bool search(int sum, int start, int end, int [] arr) 
  { 
    while (start <= end) { 
      int mid = (start + end) / 2; 
      if (arr[mid] == sum) { 
        return true; 
      } 
      else if (arr[mid] > sum) { 
        end = mid - 1; 
      } 
      else { 
        start = mid + 1; 
      } 
    } 
    return false; 
  } 
  
  // utility function for finding 
  // triplet in array 
  static void findTriplet(int[] arr, int n) 
  { 
  
    // sort the array 
    Array.Sort(arr); 
  
    // for every element in arr 
    // check if a pair exist(in 
    // array) whose sum is equal 
    // to arr element 
    for (int i = 0; i < n; i++) { 
      for(int j=i+1;j<n;j++) 
      { 
        // finding the sum of the numbers 
        if (search((arr[i] + arr[j]), j, n - 1, arr)) { 
  
          // pair found 
          Console.WriteLine("Numbers are "
                            + arr[i] + " " + arr[j] 
                            + " " + (arr[i]+arr[j])); 
          return; 
        } 
      } 
    }     
  
    // no such triplet is found in array 
    Console.WriteLine("No such triplet exists"); 
  } 
  
  // driver program 
  public static void Main() 
  { 
    int[] arr = { 5, 32, 1, 7, 10, 50, 
                 19, 21, 2 }; 
    int n = arr.Length; 
  
    findTriplet(arr, n); 
  } 
} 
  
// This code is contributed by Aarti_Rathi

Javascript

<script> 
  
// Javascript program to find three numbers 
// such that sum of two makes the 
// third element in array 
bool search(sum, start, end, arr) 
{ 
    while (start <= end) { 
        let mid = (start + end) / 2; 
        if (arr[mid] == sum) { 
            return true; 
        } 
        else if (arr[mid] > sum) { 
            end = mid - 1; 
        } 
        else { 
            start = mid + 1; 
        } 
    } 
    return false; 
} 
  
// Utility function for finding 
// triplet in array 
function findTriplet(arr, n) 
{ 
    // sort the array 
    arr.sort((a,b) => a-b); 
  
    // initialising nested loops 
    for (let i = 0; i < n; i++) { 
        for (let j = i + 1; j < n; j++) { 
            if (search((arr[i] + arr[j]), j, n - 1, arr)) { 
                document.write("numbers are " + arr[i] + 
                " " + arr[j] + " " + ( arr[i] + arr[j] ) + "<br>"); 
            } 
        } 
    } 
    // No such triplet is found in array 
    document.write("No such triplet exists"); 
} 
  
// driver program 
    let arr = [ 5, 32, 1, 7, 10, 50, 19, 21, 2 ]; 
    let n = arr.length; 
  
    findTriplet(arr, n); 
  
// This code is contributed by Sarthak Delori 
</script> 

Output

Numbers are: 2 5 7

Time Complexity: O(N^2*log N)
Auxiliary Space: O(1)

Suggest improvement

Closest product pair in an array

Check if a given string is sum-string

Share your thoughts in the comments

Find a triplet such that sum of two equals to third element

C++

Java

Python3

C#

Javascript

C++

Java

Python

C#

PHP

Javascript

C++

Java

Python3

C#

Javascript

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?