Backtracking meaning in DSA

Last Updated : 21 Feb, 2023

Backtracking can be defined as a general algorithmic technique that considers searching every possible combination in order to solve a computational problem.

Backtracking simple structure is shown like the following:

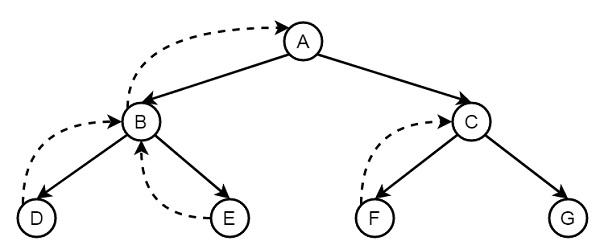
Structure of Backtracking

Properties of Backtracking:

Incremental construction: Backtracking builds a solution incrementally by constructing a partial solution and expanding it until a complete solution is found or it becomes clear that no solution exists.
Reversibility: Backtracking is reversible, as it can backtrack to a previous state and try a different path when it reaches a dead end.
Optimal solution: Backtracking can guarantee an optimal solution if the problem has a well-defined goal and optimal solution, as it explores the entire search space.
Simplicity: Backtracking is a simple approach for solving problems, as it avoids the need for complex data structures or algorithms and can be easily implemented using a simple recursive approach.

Advantages of Backtracking:

Flexibility: Backtracking can be used to solve a wide range of problems, from simple puzzles like the N-Queens problem to complex combinatorial optimization problems. It can be adapted to various constraints and problem-specific requirements.
Pruning: Backtracking can be optimized through pruning, which involves avoiding certain branches of the search tree that are not likely to lead to a solution. This can greatly reduce the search space and speed up the solution time.
Concurrent execution: Backtracking algorithms can be parallelized and executed in multiple threads, as each recursive call can be executed independently. This can greatly speed up the solution time

Disadvantages of Backtracking:

Time complexity: Backtracking can be very slow for large problems, as it explores a large search space that may contain many dead ends. This can result in a high time complexity, especially if the problem has a large number of constraints and a complex search space.
Space complexity: Backtracking can also be memory-intensive, as it requires storing the state of the partial solution at each step of the search. This can result in a high space complexity, especially for problems with a large number of variables and constraints.
Inefficiency: Backtracking can be inefficient, as it may explore the same parts of the search space multiple times. This can result in a large number of redundant calculations, which can significantly slow down the solution time.
Limited applicability: Backtracking is not suitable for problems with real-time constraints, as it may take a long time to find a solution. Additionally, it may not be appropriate for problems with continuous variables, as it can only handle discrete variables and constraints.

Application of Backtracking:

Here are five different fields in which backtracking can be used to solve problems:

Computer Science: Backtracking is commonly used in computer science to solve a wide range of problems, including search algorithms, constraint satisfaction problems, and combinatorial optimization problems.
Mathematics: Backtracking can be used in mathematics to solve a variety of problems, including those related to graph theory, number theory, and combinatorics.
Artificial Intelligence: Backtracking is a key technique used in artificial intelligence to solve problems related to planning, decision-making, and optimization. Examples include pathfinding, route planning, and constraint satisfaction problems in robotics and other AI applications.
Natural Language Processing: Backtracking can be used in natural language processing to solve problems related to parsing and semantic analysis.