Tree Traversal Techniques – Data Structure and Algorithm Tutorials
Last Updated :
28 Nov, 2023
Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways.
A Tree Data Structure can be traversed in following ways:
- Depth First Search or DFS
- Inorder Traversal
- Preorder Traversal
- Postorder Traversal
- Level Order Traversal or Breadth First Search or BFS
- Boundary Traversal
- Diagonal Traversal
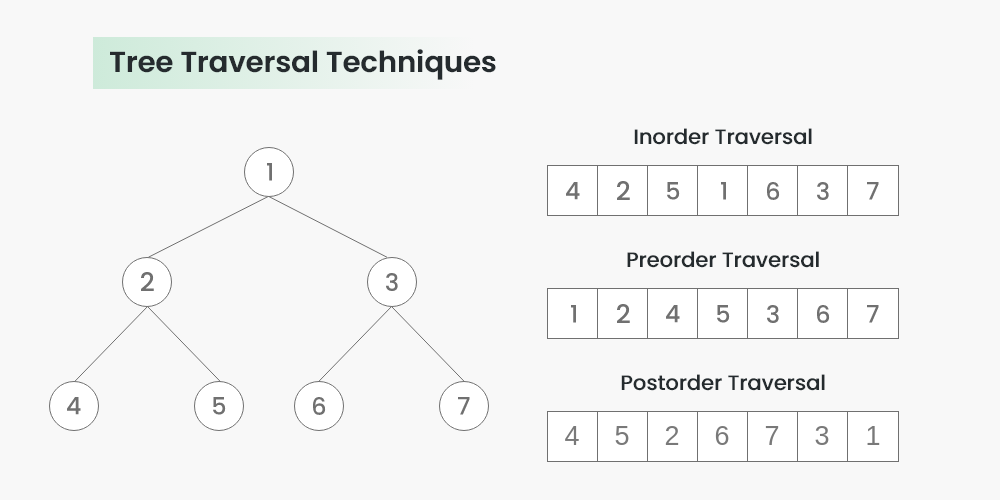
Tree Traversal
Algorithm Inorder(tree)
- Traverse the left subtree, i.e., call Inorder(left->subtree)
- Visit the root.
- Traverse the right subtree, i.e., call Inorder(right->subtree)
Uses of Inorder Traversal:
In the case of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order. To get nodes of BST in non-increasing order, a variation of Inorder traversal where Inorder traversal is reversed can be used.
Code implementation of Inorder traversal.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
};
Node* newNode(int data)
{
Node* temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
void printInorder(struct Node* node)
{
if (node == NULL)
return;
printInorder(node->left);
cout << node->data << " ";
printInorder(node->right);
}
int main()
{
struct Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Inorder traversal of binary tree is \n";
printInorder(root);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node* left;
struct node* right;
};
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
void printInorder(struct node* node)
{
if (node == NULL)
return;
printInorder(node->left);
printf("%d ", node->data);
printInorder(node->right);
}
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("Inorder traversal of binary tree is \n");
printInorder(root);
getchar();
return 0;
}
|
Java
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree() { root = null; }
void printInorder(Node node)
{
if (node == null)
return;
printInorder(node.left);
System.out.print(node.key + " ");
printInorder(node.right);
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println(
"Inorder traversal of binary tree is ");
tree.printInorder(tree.root);
}
}
|
Python3
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
def printInorder(root):
if root:
printInorder(root.left)
print(root.val, end=" "),
printInorder(root.right)
if __name__ == "__main__":
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print("Inorder traversal of binary tree is")
printInorder(root)
|
C#
using System;
class Node {
public int key;
public Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree() { root = null; }
void printInorder(Node node)
{
if (node == null)
return;
printInorder(node.left);
Console.Write(node.key + " ");
printInorder(node.right);
}
void printInorder() { printInorder(root); }
static public void Main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("Inorder traversal "
+ "of binary tree is ");
tree.printInorder();
}
}
|
Javascript
class Node {
constructor(val) {
this.key = val;
this.left = null;
this.right = null;
}
}
var root = null;
function printInorder(node) {
if (node == null)
return;
printInorder(node.left);
console.log(node.key + " ");
printInorder(node.right);
}
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
console.log("Inorder traversal of binary tree is ");
printInorder(root);
|
Output
Inorder traversal of binary tree is
4 2 5 1 3
Time Complexity: O(N)
Auxiliary Space: If we don’t consider the size of the stack for function calls then O(1) otherwise O(h) where h is the height of the tree.
Algorithm Preorder(tree)
- Visit the root.
- Traverse the left subtree, i.e., call Preorder(left->subtree)
- Traverse the right subtree, i.e., call Preorder(right->subtree)
Uses of Preorder:
Preorder traversal is used to create a copy of the tree. Preorder traversal is also used to get prefix expressions on an expression tree.
Code implementation of Preorder traversal:
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
};
Node* newNode(int data)
{
Node* temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
void printPreorder(struct Node* node)
{
if (node == NULL)
return;
cout << node->data << " ";
printPreorder(node->left);
printPreorder(node->right);
}
int main()
{
struct Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Preorder traversal of binary tree is \n";
printPreorder(root);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node* left;
struct node* right;
};
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
void printPreorder(struct node* node)
{
if (node == NULL)
return;
printf("%d ", node->data);
printPreorder(node->left);
printPreorder(node->right);
}
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("Preorder traversal of binary tree is \n");
printPreorder(root);
getchar();
return 0;
}
|
Java
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree() { root = null; }
void printPreorder(Node node)
{
if (node == null)
return;
System.out.print(node.key + " ");
printPreorder(node.left);
printPreorder(node.right);
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println(
"Preorder traversal of binary tree is ");
tree.printPreorder(tree.root);
}
}
|
Python3
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
def printPreorder(root):
if root:
print(root.val, end=" "),
printPreorder(root.left)
printPreorder(root.right)
if __name__ == "__main__":
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print("Preorder traversal of binary tree is")
printPreorder(root)
|
C#
using System;
class Node {
public int key;
public Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree() { root = null; }
void printPreorder(Node node)
{
if (node == null)
return;
Console.Write(node.key + " ");
printPreorder(node.left);
printPreorder(node.right);
}
static public void Main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("Preorder traversal "
+ "of binary tree is ");
tree.printPreorder(tree.root);
}
}
|
Javascript
class Node {
constructor(val) {
this.key = val;
this.left = null;
this.right = null;
}
}
var root = null;
function printPreorder(node) {
if (node == null)
return;
document.write(node.key + " ");
printPreorder(node.left);
printPreorder(node.right);
}
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
console.log("Preorder traversal of binary tree is ");
printPreorder(root);
|
Output
Preorder traversal of binary tree is
1 2 4 5 3
Time Complexity: O(N)
Auxiliary Space: If we don’t consider the size of the stack for function calls then O(1) otherwise O(h) where h is the height of the tree.
Algorithm Postorder(tree)
- Traverse the left subtree, i.e., call Postorder(left->subtree)
- Traverse the right subtree, i.e., call Postorder(right->subtree)
- Visit the root
Uses of Postorder:
Postorder traversal is used to delete the tree. Please see the question for the deletion of a tree for details. Postorder traversal is also useful to get the postfix expression of an expression tree
Below is the implementation of the above traversal methods:
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
};
Node* newNode(int data)
{
Node* temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
void printPostorder(struct Node* node)
{
if (node == NULL)
return;
printPostorder(node->left);
printPostorder(node->right);
cout << node->data << " ";
}
int main()
{
struct Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Postorder traversal of binary tree is \n";
printPostorder(root);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node* left;
struct node* right;
};
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
void printPostorder(struct node* node)
{
if (node == NULL)
return;
printPostorder(node->left);
printPostorder(node->right);
printf("%d ", node->data);
}
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("Postorder traversal of binary tree is \n");
printPostorder(root);
getchar();
return 0;
}
|
Java
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree() { root = null; }
void printPostorder(Node node)
{
if (node == null)
return;
printPostorder(node.left);
printPostorder(node.right);
System.out.print(node.key + " ");
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println(
"Postorder traversal of binary tree is ");
tree.printPostorder(tree.root);
}
}
|
Python3
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
def printPostorder(root):
if root:
printPostorder(root.left)
printPostorder(root.right)
print(root.val, end=" "),
if __name__ == "__main__":
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print("Postorder traversal of binary tree is")
printPostorder(root)
|
C#
using System;
class Node {
public int key;
public Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree() { root = null; }
void printPostorder(Node node)
{
if (node == null)
return;
printPostorder(node.left);
printPostorder(node.right);
Console.Write(node.key + " ");
}
static public void Main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("Postorder traversal "
+ "of binary tree is ");
tree.printPostorder(tree.root);
}
}
|
Javascript
class Node {
constructor(val) {
this.key = val;
this.left = null;
this.right = null;
}
}
var root = null;
function printPostorder(node) {
if (node == null)
return;
printPostorder(node.left);
printPostorder(node.right);
console.log(node.key + " ");
}
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
console.log("Postorder traversal of binary tree is ");
printPostorder(root);
|
Output
Postorder traversal of binary tree is
4 5 2 3 1
Some other Tree Traversals Techniques:
Some of the other tree traversals are:
For each node, first, the node is visited and then it’s child nodes are put in a FIFO queue. Then again the first node is popped out and then it’s child nodes are put in a FIFO queue and repeat until queue becomes empty.
Example:
Input:
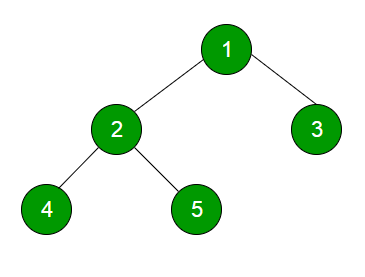
Level Order Treversal:
1
2 3
4 5
The Boundary Traversal of a Tree includes:
- left boundary (nodes on left excluding leaf nodes)
- leaves (consist of only the leaf nodes)
- right boundary (nodes on right excluding leaf nodes)

In the Diagonal Traversal of a Tree, all the nodes in a single diagonal will be printed one by one.
Input :
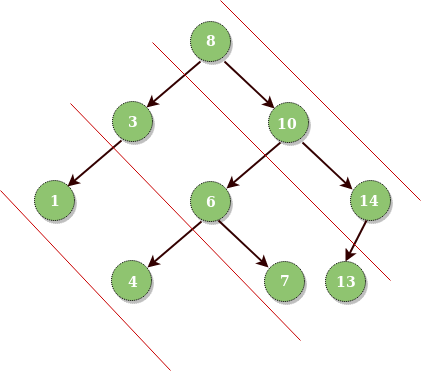
Diagonal Traversal of binary tree:
8 10 14
3 6 7 13
1 4
Some other important Tutorials:
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...