Searching Elements in an Array | Array Operations

Last Updated : 22 Jan, 2024

In this post, we will look into search operation in an Array, i.e., how to search an element in an Array, such as:

Searching in an Unsorted Array using Linear Search
Searching in a Sorted Array using Linear Search
Searching in a Sorted Array using Binary Search
Searching in an Sorted Array using Fibonacci Search

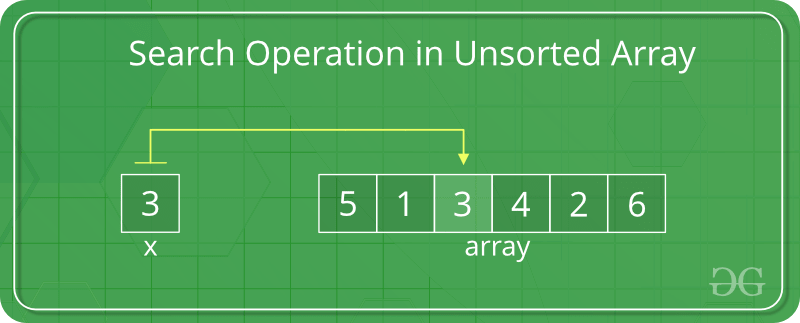
Searching operations in an Unsorted Array using Linear Search

In an unsorted array, the search operation can be performed by linear traversal from the first element to the last element, i.e. Linear Search

Coding implementation of the search operation:

C++

// C++ program to implement linear
// search in unsorted array
#include <bits/stdc++.h>
using namespace std;
 
// Function to implement search operation
int findElement(int arr[], int n, int key)
{
    int i;
    for (i = 0; i < n; i++)
        if (arr[i] == key)
            return i;
 
    // If the key is not found
    return -1;
}
 
// Driver's Code
int main()
{
    int arr[] = { 12, 34, 10, 6, 40 };
    int n = sizeof(arr) / sizeof(arr[0]);
 
    // Using a last element as search element
    int key = 40;
 
    // Function call
    int position = findElement(arr, n, key);
 
    if (position == -1)
        cout << "Element not found";
    else
        cout << "Element Found at Position: "
             << position + 1;
 
    return 0;
}
 
// This code is contributed
// by Akanksha Rai

C

// C program to implement linear
// search in unsorted array
#include <stdio.h>
 
// Function to implement search operation
int findElement(int arr[], int n, int key)
{
    int i;
    for (i = 0; i < n; i++)
        if (arr[i] == key)
            return i;
 
    // If the key is not found
    return -1;
}
 
// Driver's Code
int main()
{
    int arr[] = { 12, 34, 10, 6, 40 };
    int n = sizeof(arr) / sizeof(arr[0]);
 
    // Using a last element as search element
    int key = 40;
 
    // Function call
    int position = findElement(arr, n, key);
 
    if (position == -1)
        printf("Element not found");
    else
        printf("Element Found at Position: %d",
               position + 1);
 
    return 0;
}

Java

// Java program to implement linear
// search in unsorted arrays
 
class Main {
 
    // Function to implement
    // search operation
    static int findElement(int arr[], int n, int key)
    {
        for (int i = 0; i < n; i++)
            if (arr[i] == key)
                return i;
 
        // If the key is not found
        return -1;
    }
 
    // Driver's Code
    public static void main(String args[])
    {
        int arr[] = { 12, 34, 10, 6, 40 };
        int n = arr.length;
 
        // Using a last element as search element
        int key = 40;
 
        // Function call
        int position = findElement(arr, n, key);
 
        if (position == -1)
            System.out.println("Element not found");
        else
            System.out.println("Element Found at Position: "
                               + (position + 1));
    }
}

Python3

# Python program for searching in
# unsorted array
 
 
def findElement(arr, n, key):
    for i in range(n):
        if (arr[i] == key):
            return i
 
    # If the key is not found
    return -1
 
 
# Driver's code
if __name__ == '__main__':
    arr = [12, 34, 10, 6, 40]
    key = 40
    n = len(arr)
 
    # search operation
    index = findElement(arr, n, key)
    if index != -1:
        print("Element Found at position: " + str(index + 1))
    else:
        print("Element not found")
 
    # Thanks to Aditi Sharma for contributing
    # this code

C#

// C# program to implement linear
// search in unsorted arrays
using System;
 
class main {
    // Function to implement
    // search operation
    static int findElement(int[] arr, int n, int key)
    {
        for (int i = 0; i < n; i++)
            if (arr[i] == key)
                return i;
 
        // If the key is not found
        return -1;
    }
 
    // Driver Code
    public static void Main()
    {
        int[] arr = { 12, 34, 10, 6, 40 };
        int n = arr.Length;
 
        // Using a last element as
        // search element
        int key = 40;
        int position = findElement(arr, n, key);
 
        if (position == -1)
            Console.WriteLine("Element not found");
        else
            Console.WriteLine("Element Found at Position: "
                              + (position + 1));
    }
}
 
//  This code is contributed by vt_m.

Javascript

// Javascript program to implement linear 
// search in unsorted array
 
 
// Function to implement search operation 
function findElement( arr, n, key)
{
    let i;
    for (i = 0; i < n; i++)
        if (arr[i] == key)
            return i;
 
    return -1;
}
 
 
     
    // Driver program
     
    let arr = [12, 34, 10, 6, 40];
    let n = arr.length;
 
    // Using a last element as search element
    let key = 40;
    let position = findElement(arr, n, key);
 
    if (position == - 1)
        document.write("Element not found");
    else
        document.write("Element Found at Position: " 
             + (position + 1));

PHP

<?php
// PHP program to implement linear 
// search in unsorted array
 
// Function to implement
// search operation 
function findElement($arr, $n, $key)
{
    $i;
    for ($i = 0; $i < $n; $i++)
        if ($arr[$i] == $key)
            return $i;
     
      // If the key is not found
    return -1;
}
 
// Driver Code
$arr = array(12, 34, 10, 6, 40);
$n = sizeof($arr);
 
// Using a last element
// as search element
$key = 40;
$position = findElement($arr, $n, $key);
 
if ($position == - 1)
    echo("Element not found");
else
    echo("Element Found at Position: " . ($position + 1));
 
// This code is contributed by Ajit.
?>

Output

Element Found at Position: 5

Time Complexity: O(N)
Auxiliary Space: O(1)

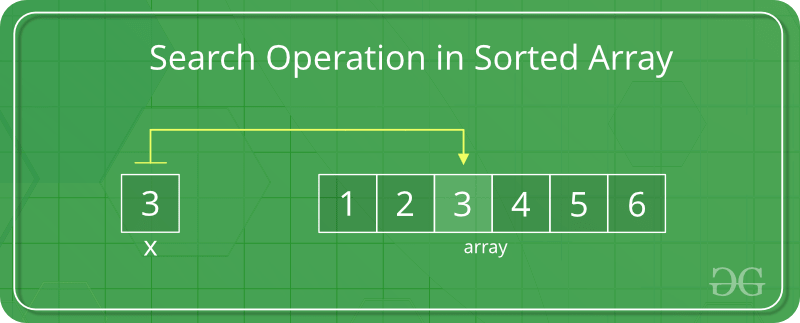
Searching in a Sorted Array using Linear Search

In a sorted array, the most trivial method for search operation is by using Linear Search.

Below is the implementation of the above approach:

C++

// C++ program to implement linear
// search in sorted array
#include <bits/stdc++.h>
using namespace std;
 
// Function to implement search operation
int findElement(int arr[], int n, int key)
{
    int i;
    for (i = 0; i < n; i++)
        if (arr[i] == key)
            return i;
 
    // If the key is not found
    return -1;
}
 
// Driver's Code
int main()
{
    int arr[] = { 5, 6, 7, 8, 9, 10 };
    int n = sizeof(arr) / sizeof(arr[0]);
 
    // Using a last element as search element
    int key = 10;
 
    // Function call
    int position = findElement(arr, n, key);
 
    if (position == -1)
        cout << "Element not found";
    else
        cout << "Element Found at Position: "
             << position + 1;
 
    return 0;
}
 
// This code is contributed
// by Akanksha Rai

C

// C program to implement linear
// search in sorted array
#include <stdio.h>
 
// Function to implement search operation
int findElement(int arr[], int n, int key)
{
    int i;
    for (i = 0; i < n; i++)
        if (arr[i] == key)
            return i;
 
    // If the key is not found
    return -1;
}
 
// Driver's Code
int main()
{
    int arr[] = { 5, 6, 7, 8, 9, 10 };
    int n = sizeof(arr) / sizeof(arr[0]);
 
    // Using a last element as search element
    int key = 10;
 
    // Function call
    int position = findElement(arr, n, key);
 
    if (position == -1)
        printf("Element not found");
    else
        printf("Element Found at Position: %d",
               position + 1);
 
    return 0;
}

Java

// Java program to implement linear
// search in sorted arrays
 
class Main {
 
    // Function to implement
    // search operation
    static int findElement(int arr[], int n, int key)
    {
        for (int i = 0; i < n; i++)
            if (arr[i] == key)
                return i;
 
        // If the key is not found
        return -1;
    }
 
    // Driver's Code
    public static void main(String args[])
    {
        int arr[] = { 5, 6, 7, 8, 9, 10 };
        int n = arr.length;
 
        // Using a last element as search element
        int key = 10;
 
        // Function call
        int position = findElement(arr, n, key);
 
        if (position == -1)
            System.out.println("Element not found");
        else
            System.out.println("Element Found at Position: "
                               + (position + 1));
    }
}

Python3

# Python program for searching in
# sorted array
 
 
def findElement(arr, n, key):
    for i in range(n):
        if (arr[i] == key):
            return i
 
    # If the key is not found
    return -1
 
 
# Driver's code
if __name__ == '__main__':
    arr = [5, 6, 7, 8, 9, 10]
    key = 10
    n = len(arr)
 
    # search operation
    index = findElement(arr, n, key)
    if index != -1:
        print("Element Found at position: " + str(index + 1))
    else:
        print("Element not found")
 
    # Thanks to Aditi Sharma for contributing
    # this code

C#

// C# program to implement linear
// search in sorted arrays
using System;
 
class main {
    // Function to implement
    // search operation
    static int findElement(int[] arr, int n, int key)
    {
        for (int i = 0; i < n; i++)
            if (arr[i] == key)
                return i;
 
        // If the key is not found
        return -1;
    }
 
    // Driver Code
    public static void Main()
    {
        int[] arr = { 5, 6, 7, 8, 9, 10 };
        int n = arr.Length;
 
        // Using a last element as
        // search element
        int key = 10;
        int position = findElement(arr, n, key);
 
        if (position == -1)
            Console.WriteLine("Element not found");
        else
            Console.WriteLine("Element Found at Position: "
                              + (position + 1));
    }
}
 
//  This code is contributed by vt_m.

Javascript

// Javascript program to implement linear 
// search in sorted array
 
 
// Function to implement search operation 
function findElement( arr, n, key)
{
    let i;
    for (i = 0; i < n; i++)
        if (arr[i] == key)
            return i;
 
    return -1;
}
 
 
     
    // Driver program
     
    let arr = [5, 6, 7, 8, 9, 10];
    let n = arr.length;
 
    // Using a last element as search element
    let key = 10;
    let position = findElement(arr, n, key);
 
    if (position == - 1)
        document.write("Element not found");
    else
        document.write("Element Found at Position: " 
             + (position + 1));

PHP

<?php
// PHP program to implement linear 
// search in sorted array
 
// Function to implement
// search operation 
function findElement($arr, $n, $key)
{
    $i;
    for ($i = 0; $i < $n; $i++)
        if ($arr[$i] == $key)
            return $i;
     
      // If the key is not found
    return -1;
}
 
// Driver Code
$arr = array(5, 6, 7, 8, 9, 10);
$n = sizeof($arr);
 
// Using a last element
// as search element
$key = 10;
$position = findElement($arr, $n, $key);
 
if ($position == - 1)
    echo("Element not found");
else
    echo("Element Found at Position: " . ($position + 1));
 
// This code is contributed by Ajit.
?>

Output

Element Found at Position: 6

Time Complexity: O(N)
Auxiliary Space: O(1)

Searching in a Sorted Array using Binary Search

In a sorted array, the search operation can be performed efficiently by using binary search.

Below is the implementation of the above approach:

C++

// C++ program to implement binary search in sorted array
#include <bits/stdc++.h>
using namespace std;
 
int binarySearch(int arr[], int low, int high, int key)
{
    if (high < low)
        return -1;
    int mid = (low + high) / 2; /*low + (high - low)/2;*/
    if (key == arr[mid])
        return mid;
    if (key > arr[mid])
        return binarySearch(arr, (mid + 1), high, key);
    return binarySearch(arr, low, (mid - 1), key);
}
 
/* Driver code */
int main()
{
    // Let us search 3 in below array
    int arr[] = { 5, 6, 7, 8, 9, 10 };
    int n, key;
 
    n = sizeof(arr) / sizeof(arr[0]);
    key = 10;
 
    // Function call
    cout << "Index: " << binarySearch(arr, 0, n - 1, key)
         << endl;
    return 0;
}
 
// This code is contributed by NamrataSrivastava1

C

// C program to implement binary search in sorted array
#include <stdio.h>
 
int binarySearch(int arr[], int low, int high, int key)
{
    if (high < low)
        return -1;
    int mid = (low + high) / 2; /*low + (high - low)/2;*/
    if (key == arr[mid])
        return mid;
    if (key > arr[mid])
        return binarySearch(arr, (mid + 1), high, key);
    return binarySearch(arr, low, (mid - 1), key);
}
 
/* Driver Code */
int main()
{
    // Let us search 3 in below array
    int arr[] = { 5, 6, 7, 8, 9, 10 };
    int n, key;
 
    n = sizeof(arr) / sizeof(arr[0]);
    key = 10;
 
    // Function call
    printf("Index: %d\n", binarySearch(arr, 0, n - 1, key));
    return 0;
}

Java

// Java program to implement binary
// search in a sorted array
 
class Main {
    // function to implement
    // binary search
    static int binarySearch(int arr[], int low, int high,
                            int key)
    {
        if (high < low)
            return -1;
 
        /*low + (high - low)/2;*/
        int mid = (low + high) / 2;
        if (key == arr[mid])
            return mid;
        if (key > arr[mid])
            return binarySearch(arr, (mid + 1), high, key);
        return binarySearch(arr, low, (mid - 1), key);
    }
 
    /* Driver Code*/
    public static void main(String[] args)
    {
        int arr[] = { 5, 6, 7, 8, 9, 10 };
        int n, key;
        n = arr.length - 1;
        key = 10;
 
        // Function call
        System.out.println("Index: "
                           + binarySearch(arr, 0, n, key));
    }
}

Python3

# python 3  program to implement
# binary search in sorted array
 
 
def binarySearch(arr, low, high, key):
 
    mid = (low + high)/2
 
    if (key == arr[int(mid)]):
        return mid
 
    if (key > arr[int(mid)]):
        return binarySearch(arr,
                            (mid + 1), high, key)
 
    if (key < arr[int(mid)]):
        return binarySearch(arr, low, (mid-1), key)
 
    return 0
 
 
# Driver code
if __name__ == "__main__":
    # Let us search 3 in below array
    arr = [5, 6, 7, 8, 9, 10]
    n = len(arr)
    key = 10
 
    # Function call
    print("Index:", int(binarySearch(arr, 0, n-1, key)))
 
# This code is contributed by
# Smitha Dinesh Semwal

C#

// C# program to implement binary
// search in a sorted array
 
using System;
 
public class GFG {
 
    // function to implement
    // binary search
    public static int binarySearch(int[] arr, int low,
                                   int high, int key)
    {
        if (high < low) {
            return -1;
        }
 
        int mid = (low + high) / 2;
        if (key == arr[mid]) {
            return mid;
        }
        if (key > arr[mid]) {
            return binarySearch(arr, (mid + 1), high, key);
        }
        return binarySearch(arr, low, (mid - 1), key);
    }
 
    /* Driver Code */
    public static void Main(string[] args)
    {
        int[] arr = new int[] { 5, 6, 7, 8, 9, 10 };
        int n, key;
        n = arr.Length;
        key = 10;
 
        // Function call
        Console.WriteLine(
            "Index: " + binarySearch(arr, 0, n - 1, key));
    }
}
 
// This code is contributed by Shrikant13

Javascript

<script>
 
 
// Javascript program to implement 
// binary search in sorted array
 
function binarySearch( arr, low, high, key)
{
    if (high < low)
        return -1;
        /*low + (high - low)/2;*/
    let mid = Math.trunc((low + high) / 2); 
    if (key == arr[mid])
        return mid;
    if (key > arr[mid])
        return binarySearch(arr, (mid + 1), high, key);
    return binarySearch(arr, low, (mid - 1), key);
}
 
     
    // Driver program
     
    // Let us search 3 in below array
    let arr = [ 5, 6, 7, 8, 9, 10 ];
    let n, key;
 
    n = arr.length;
    key = 10;
 
    document.write( "Index: " + binarySearch(arr, 0, n - 1, key)
    + "</br>");
     
     
</script>

PHP

<?php
// PHP program to implement
// binary search in sorted array
 
function binarySearch($arr, $low, 
                      $high, $key) 
{
    if ($high < $low) 
    return -1;
     
    $mid = (int)($low + $high) / 2;
     
    if ($key == $arr[(int)$mid])
        return $mid;
     
    if ($key > $arr[(int)$mid]) 
        return binarySearch($arr, ($mid + 1), 
                            $high, $key);
     
    return (binarySearch($arr, $low, 
                        ($mid -1), $key));
}
 
// Driver Code
 
// Let us search 3 in below array
$arr = array(5, 6, 7, 8, 9, 10);
$n = count($arr);
$key = 10;
 
// Function call
echo "Index: ", (int)binarySearch($arr, 0, 
                                  $n-1, $key);
 
// This code is contributed by
// Srathore
?>

Output

Index: 5

Time Complexity: O(log(n)) Using Binary Search
Auxiliary Space: O(log(n)) due to recursive calls, otherwise iterative version uses Auxiliary Space of O(1).

Searching in a Sorted Array using Fibonacci Search

Fibonacci Search is a comparison-based technique that uses Fibonacci numbers to search an element in a sorted array.

Untitled

Below is the implementation of the above approach:

C++

// C++ program of the above approach
#include <iostream>
#include <vector>
using std::cout;
 
//  Utility function to find minimum of two elements
int minimum(int x, int y) { return (x < y) ? x : y; }
 
/* Returns index of x if present,  else returns -1 */
int fibonacciSearch(int arr[], int x, int n)
{
    /* Initialize fibonacci numbers */
    int fibMMm2 = 0; // (m-2)'th Fibonacci No.
    int fibMMm1 = 1; // (m-1)'th Fibonacci No.
    int fibM = fibMMm2 + fibMMm1; // m'th Fibonacci
 
    /* fibM is going to store the smallest Fibonacci
       Number greater than or equal to n */
    while (fibM < n) {
        fibMMm2 = fibMMm1;
        fibMMm1 = fibM;
        fibM = fibMMm2 + fibMMm1;
    }
 
    // Marks the eliminated range from front
    int offset = -1;
 
    /* while there are elements to be inspected. Note that
       we compare arr[fibMm2] with x. When fibM becomes 1,
       fibMm2 becomes 0 */
    while (fibM > 1) {
        // Check if fibMm2 is a valid location
        int i = minimum(offset + fibMMm2, n - 1);
 
        /* If x is greater than the value at index fibMm2,
           cut the subarray array from offset to i */
        if (arr[i] < x) {
            fibM = fibMMm1;
            fibMMm1 = fibMMm2;
            fibMMm2 = fibM - fibMMm1;
            offset = i;
        }
 
        /* If x is greater than the value at index fibMm2,
           cut the subarray after i+1  */
        else if (arr[i] > x) {
            fibM = fibMMm2;
            fibMMm1 = fibMMm1 - fibMMm2;
            fibMMm2 = fibM - fibMMm1;
        }
 
        /* element found. return index */
        else
            return i;
    }
 
    /* comparing the last element with x */
    if (fibMMm1 && arr[offset + 1] == x)
        return offset + 1;
 
    /*element not found. return -1 */
    return -1;
}
 
// Driver Code
int main()
{
    int arr[] = { 10, 22, 35, 40, 45,  50,
                  80, 82, 85, 90, 100, 235 };
    int n = sizeof(arr) / sizeof(arr[0]);
    int x = 235;
    int ind = fibonacciSearch(arr, x, n);
    if (ind >= 0)
        cout << "Found at index: " << ind;
    else
        cout << x << " isn't present in the array";
 
    return 0;
}
 
// This code is contributed by sourabh_jain.

C

// C program for Fibonacci Search
#include <stdio.h>
 
// Function to find minimum of two elements
int minimum(int x, int y) { return (x <= y) ? x : y; }
 
/* Returns index of x if present, else returns -1 */
int fibonacciSearch(int arr[], int x, int n)
{
    /* Initialize Fibonacci numbers */
    int fibMMm2 = 0; // (m-2)'th Fibonacci number
    int fibMMm1 = 1; // (m-1)'th Fibonacci number
    int fibM = fibMMm2 + fibMMm1; // m'th Fibonacci number
 
    /* fibM is going to store the smallest Fibonacci
     number greater than or equal to n */
    while (fibM < n) {
        fibMMm2 = fibMMm1;
        fibMMm1 = fibM;
        fibM = fibMMm2 + fibMMm1;
    }
 
    // Marks the eliminated range from front
    int offset = -1;
 
    /* while there are elements to be inspected. Note that
     we compare arr[fibMm2] with x. When fibM becomes 1,
     fibMm2 becomes 0 */
    while (fibM > 1) {
        // Check if fibMm2 is a valid location
        int i = minimum(offset + fibMMm2, n - 1);
 
        /* If x is greater than the value at index fibMm2,
         cut the subarray array from offset to i */
        if (arr[i] < x) {
            fibM = fibMMm1;
            fibMMm1 = fibMMm2;
            fibMMm2 = fibM - fibMMm1;
            offset = i;
        }
 
        /* If x is greater than the value at index fibMm2,
         cut the subarray after i+1 */
        else if (arr[i] > x) {
            fibM = fibMMm2;
            fibMMm1 = fibMMm1 - fibMMm2;
            fibMMm2 = fibM - fibMMm1;
        }
 
        /* element found. return index */
        else
            return i;
    }
 
    /* comparing the last element with x */
    if (fibMMm1 && arr[offset + 1] == x)
        return offset + 1;
 
    /* element not found. return -1 */
    return -1;
}
 
/* driver function */
int main(void)
{
    int arr[] = { 10, 22, 35, 40, 45,  50,
                  80, 82, 85, 90, 100, 235 };
    int n = sizeof(arr) / sizeof(arr[0]);
    int x = 235;
    int index = fibonacciSearch(arr, x, n);
    if (index >= 0)
        printf("Element found at index: %d", index);
    else
        printf("%d is not present in the array", x);
    return 0;
}
// This code is contributed by sourabh_jain.

Java

// Java program of the above approach
import java.util.*; // adding util packages
 
class FibonacciSearch {
    // Function to find the minimum of two elements
    public static int minimum(int x, int y)
    {
        return (x <= y) ? x : y;
    }
 
    /* Returns the index of x if present, else returns -1 */
    public static int fibonacciSearch(int arr[], int x,
                                      int n)
    {
        /* Initialize Fibonacci numbers */
        int fibMMm2 = 0; // (m-2)'th Fibonacci number
        int fibMMm1 = 1; // (m-1)'th Fibonacci number
        int fibM
            = fibMMm2 + fibMMm1; // m'th Fibonacci number
 
        /* fibM is going to store the smallest Fibonacci
        Number greater than or equal to n */
        while (fibM < n) {
            fibMMm2 = fibMMm1;
            fibMMm1 = fibM;
            fibM = fibMMm2 + fibMMm1;
        }
 
        // Marks the eliminated range from the front
        int offset = -1;
 
        /* While there are elements to be inspected.
        Note that we compare arr[fibMm2] with x.
        When fibM becomes 1, fibMm2 becomes 0 */
        while (fibM > 1) {
            // Check if fibMm2 is a valid location
            int i = minimum(offset + fibMMm2, n - 1);
 
            /* If x is greater than the value at index
            fibMm2,
            cut the subarray array from offset to i */
            if (arr[i] < x) {
                fibM = fibMMm1;
                fibMMm1 = fibMMm2;
                fibMMm2 = fibM - fibMMm1;
                offset = i;
            }
 
            /* If x is less than the value at index fibMm2,
            cut the subarray after i+1 */
            else if (arr[i] > x) {
                fibM = fibMMm2;
                fibMMm1 = fibMMm1 - fibMMm2;
                fibMMm2 = fibM - fibMMm1;
            }
 
            /* Element found. Return index */
            else
                return i;
        }
 
        /* Comparing the last element with x */
        if (fibMMm1 == 1 && arr[n - 1] == x)
            return n - 1;
 
        /* Element not found. Return -1 */
        return -1;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int arr[] = { 10, 22, 35, 40, 45,  50,
                      80, 82, 85, 90, 100, 235 };
        int n = 12;
        int x = 235;
        int index = fibonacciSearch(arr, x, n);
        if (index >= 0)
            System.out.print("Element found at index: "
                             + index);
        else
            System.out.print(
                x + " isn't present in the array");
    }
}
 
// This code is contributed by sourabh_jain.

Python3

# Pythin3 program of the above approach
def fibonacci_search(arr, x, n):
    # Initialize Fibonacci numbers
    fibMMm2 = 0  # (m-2)'th Fibonacci No.
    fibMMm1 = 1  # (m-1)'th Fibonacci No.
    fibM = fibMMm2 + fibMMm1  # m'th Fibonacci
 
    # fibM is going to store the smallest
    # Fibonacci Number greater than or equal to n
    while fibM < n:
        fibMMm2 = fibMMm1
        fibMMm1 = fibM
        fibM = fibMMm2 + fibMMm1
 
    # Marks the eliminated range from the front
    offset = -1
 
    # while there are elements to be inspected.
    # Note that we compare arr[fibMm2] with x.
    # When fibM becomes 1, fibMm2 becomes 0
    while fibM > 1:
        # Check if fibMm2 is a valid location
        i = min(offset + fibMMm2, n - 1)
 
        # If x is greater than the value at
        # index fibMm2, cut the subarray array
        # from offset to i
        if arr[i] < x:
            fibM = fibMMm1
            fibMMm1 = fibMMm2
            fibMMm2 = fibM - fibMMm1
            offset = i
 
        # If x is less than the value at
        # index fibMm2, cut the subarray
        # after i+1
        elif arr[i] > x:
            fibM = fibMMm2
            fibMMm1 = fibMMm1 - fibMMm2
            fibMMm2 = fibM - fibMMm1
 
        # element found. return index
        else:
            return i
 
    # comparing the last element with x
    if fibMMm1 and arr[n - 1] == x:
        return n - 1
 
    # element not found. return -1
    return -1
 
 
# Driver Code
arr = [10, 22, 35, 40, 45, 50,
       80, 82, 85, 90, 100, 235]
n = len(arr)
x = 235
index = fibonacci_search(arr, x, n)
if index >= 0:
    print("Element found at index:", index)
else:
    print(x, "isn't present in the array")
 
# This code is contributed by sourabh_jain.

C#

// C# program of the above approach
using System;
 
class GFG {
    // Function to find the minimum of two elements
    public static int Min(int x, int y)
    {
        return (x <= y) ? x : y;
    }
 
    /* Returns the index of x if present, else returns -1 */
    public static int FibonacciSearch(int[] arr, int x,
                                      int n)
    {
        /* Initialize Fibonacci numbers */
        int fibMMm2 = 0; // (m-2)'th Fibonacci number
        int fibMMm1 = 1; // (m-1)'th Fibonacci number
        int fibM = fibMMm2 + fibMMm1; // m'th Fibonacci
 
        /* fibM is going to store the smallest Fibonacci
        Number greater than or equal to n */
        while (fibM < n) {
            fibMMm2 = fibMMm1;
            fibMMm1 = fibM;
            fibM = fibMMm2 + fibMMm1;
        }
 
        // Marks the eliminated range from the front
        int offset = -1;
 
        /* While there are elements to be inspected.
        Note that we compare arr[fibMm2] with x.
        When fibM becomes 1, fibMm2 becomes 0 */
        while (fibM > 1) {
            // Check if fibMm2 is a valid location
            int i = Min(offset + fibMMm2, n - 1);
 
            /* If x is greater than the value at
            index fibMm2, cut the subarray array
            from offset to i */
            if (arr[i] < x) {
                fibM = fibMMm1;
                fibMMm1 = fibMMm2;
                fibMMm2 = fibM - fibMMm1;
                offset = i;
            }
 
            /* If x is less than the value at
            index fibMm2, cut the subarray
            after i+1 */
            else if (arr[i] > x) {
                fibM = fibMMm2;
                fibMMm1 = fibMMm1 - fibMMm2;
                fibMMm2 = fibM - fibMMm1;
            }
 
            /* Element found. Return index */
            else
                return i;
        }
 
        /* Comparing the last element with x */
        if (fibMMm1 == 1 && arr[n - 1] == x)
            return n - 1;
 
        /* Element not found. Return -1 */
        return -1;
    }
 
    // Driver code
    public static void Main()
    {
        int[] arr = { 10, 22, 35, 40, 45,  50,
                      80, 82, 85, 90, 100, 235 };
        int n = 12;
        int x = 235;
        int index = FibonacciSearch(arr, x, n);
        if (index >= 0)
            Console.Write("Element found at index: "
                          + index);
        else
            Console.Write(x
                          + " isn't present in the array");
    }
}
 
// This code is contributed by sourabh_jain.

Javascript

// JavaScript program of the above approach
 
/* Returns the index of x if present, else returns -1 */
function fibonacciSearch(arr, x, n) {
    /* Initialize Fibonacci numbers */
    let fibMMm2 = 0; // (m-2)'th Fibonacci No.
    let fibMMm1 = 1; // (m-1)'th Fibonacci No.
    let fibM = fibMMm2 + fibMMm1; // m'th Fibonacci
 
    /* fibM is going to store the smallest Fibonacci
    Number greater than or equal to n */
    while (fibM < n) {
        fibMMm2 = fibMMm1;
        fibMMm1 = fibM;
        fibM = fibMMm2 + fibMMm1;
    }
 
    // Marks the eliminated range from the front
    let offset = -1;
 
    /* While there are elements to be inspected.
    Note that we compare arr[fibMm2] with x.
    When fibM becomes 1, fibMm2 becomes 0 */
    while (fibM > 1) {
        // Check if fibMm2 is a valid location
        let i = Math.min(offset + fibMMm2, n - 1);
 
        /* If x is greater than the value at
        index fibMm2, cut the subarray array
        from offset to i */
        if (arr[i] < x) {
            fibM = fibMMm1;
            fibMMm1 = fibMMm2;
            fibMMm2 = fibM - fibMMm1;
            offset = i;
        }
 
        /* If x is less than the value at index fibMm2,
        cut the subarray after i+1 */
        else if (arr[i] > x) {
            fibM = fibMMm2;
            fibMMm1 = fibMMm1 - fibMMm2;
            fibMMm2 = fibM - fibMMm1;
        }
 
        /* Element found. Return index */
        else return i;
    }
 
    /* Comparing the last element with x */
    if (fibMMm1 && arr[n - 1] == x) {
        return n - 1;
    }
 
    /* Element not found. Return -1 */
    return -1;
}
 
/* Driver code */
let arr = [10, 22, 35, 40, 45, 50, 80, 82, 85, 90, 100, 235];
let n = arr.length;
let x = 235;
let index = fibonacciSearch(arr, x, n);
if (index >= 0) {
    document.write("Element found at index: " + index);
} else {
    document.write(x + " isn't present in the array");
}
 
// This code is contributed by sourabh_jain.

PHP

<?php
// PHP program of the above approach
 
/* Returns the index of x if present, else returns -1 */
function fibonacciSearch($arr, $x, $n)
{
    /* Initialize Fibonacci numbers */
    $fibMMm2 = 0; // (m-2)'th Fibonacci No.
    $fibMMm1 = 1; // (m-1)'th Fibonacci No.
    $fibM = $fibMMm2 + $fibMMm1; // m'th Fibonacci
 
    /* fibM is going to store the smallest Fibonacci
    Number greater than or equal to n */
    while ($fibM < $n)
    {
        $fibMMm2 = $fibMMm1;
        $fibMMm1 = $fibM;
        $fibM = $fibMMm2 + $fibMMm1;
    }
 
    // Marks the eliminated range from the front
    $offset = -1;
 
    /* While there are elements to be inspected.
    Note that we compare arr[fibMm2] with x.
    When fibM becomes 1, fibMm2 becomes 0 */
    while ($fibM > 1)
    {
        // Check if fibMm2 is a valid location
        $i = min($offset + $fibMMm2, $n - 1);
 
        /* If x is greater than the value at
        index fibMm2, cut the subarray array
        from offset to i */
        if ($arr[$i] < $x)
        {
            $fibM = $fibMMm1;
            $fibMMm1 = $fibMMm2;
            $fibMMm2 = $fibM - $fibMMm1;
            $offset = $i;
        }
 
        /* If x is less than the value at
        index fibMm2, cut the subarray
        after i+1 */
        elseif ($arr[$i] > $x)
        {
            $fibM = $fibMMm2;
            $fibMMm1 = $fibMMm1 - $fibMMm2;
            $fibMMm2 = $fibM - $fibMMm1;
        }
 
        /* Element found. Return index */
        else
            return $i;
    }
 
    /* Comparing the last element with x */
    if ($fibMMm1 == 1 && $arr[$n - 1] == $x)
        return $n - 1;
 
    /* Element not found. Return -1 */
    return -1;
}
 
/* Driver code */
$arr = array(10, 22, 35, 40, 45, 50, 80, 82, 85, 90, 100, 235);
$n = count($arr);
$x = 235;
$index = fibonacciSearch($arr, $x, $n);
if ($index >= 0)
    printf("Element found at index: " . $index);
else
    printf($x . " isn't present in the array");
?>
 
// This code is contributed by sourabh_jain.

Output

Found at index: 11

Time Complexity: O(log(n)) Using Fibonacci Search
Auxiliary Space: O(1) Using Fibonacci Search

Suggest improvement

Introduction to Invariants and Monovariants

Count triplets with specific property

Share your thoughts in the comments

Searching Elements in an Array | Array Operations

Searching operations in an Unsorted Array using Linear Search

C++

C

Java

Python3

C#

Javascript

PHP

Searching in a Sorted Array using Linear Search

C++

C

Java

Python3

C#

Javascript

PHP

Searching in a Sorted Array using Binary Search

C++

C

Java

Python3

C#

Javascript

PHP

Searching in a Sorted Array using Fibonacci Search

C++

C

Java

Python3

C#

Javascript

PHP

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?