Equilibrium index of an array
Last Updated :
15 Feb, 2023
Given a sequence arr[] of size n, Write a function int equilibrium(int[] arr, int n) that returns an equilibrium index (if any) or -1 if no equilibrium index exists.
The equilibrium index of an array is an index such that the sum of elements at lower indexes is equal to the sum of elements at higher indexes.
Examples:
Input: A[] = {-7, 1, 5, 2, -4, 3, 0}
Output: 3
3 is an equilibrium index, because:
A[0] + A[1] + A[2] = A[4] + A[5] + A[6]
Input: A[] = {1, 2, 3}
Output: -1
Naive approach: To solve the problem follow the below idea:
Use two loops. The Outer loop iterates through all the element and inner loop finds out whether the current index picked by the outer loop is equilibrium index or not
Steps to solve the problem:
1. iterate through i=1 to n:
*declare a leftsum variable to zero.
*iterate through 0 till i and add arr[i] to leftsum.
*declare a rightsum variable to zero.
*iterate through i+1 till n and add arr[i] to rightsum.
*check if leftsum is equal to rightsum than return arr[i].
2. return -1 in case of no point.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int equilibrium(int arr[], int n)
{
int i, j;
int leftsum, rightsum;
for (i = 0; i < n; ++i) {
leftsum = 0;
for (j = 0; j < i; j++)
leftsum += arr[j];
rightsum = 0;
for (j = i + 1; j < n; j++)
rightsum += arr[j];
if (leftsum == rightsum)
return i;
}
return -1;
}
int main()
{
int arr[] = { -7, 1, 5, 2, -4, 3, 0 };
int arr_size = sizeof(arr) / sizeof(arr[0]);
cout << equilibrium(arr, arr_size);
return 0;
}
|
C
#include <stdio.h>
int equilibrium(int arr[], int n)
{
int i, j;
int leftsum, rightsum;
for (i = 0; i < n; ++i) {
leftsum = 0;
for (j = 0; j < i; j++)
leftsum += arr[j];
rightsum = 0;
for (j = i + 1; j < n; j++)
rightsum += arr[j];
if (leftsum == rightsum)
return i;
}
return -1;
}
int main()
{
int arr[] = { -7, 1, 5, 2, -4, 3, 0 };
int arr_size = sizeof(arr) / sizeof(arr[0]);
printf("%d", equilibrium(arr, arr_size));
getchar();
return 0;
}
|
Java
class EquilibriumIndex {
int equilibrium(int arr[], int n)
{
int i, j;
int leftsum, rightsum;
for (i = 0; i < n; ++i) {
leftsum = 0;
for (j = 0; j < i; j++)
leftsum += arr[j];
rightsum = 0;
for (j = i + 1; j < n; j++)
rightsum += arr[j];
if (leftsum == rightsum)
return i;
}
return -1;
}
public static void main(String[] args)
{
EquilibriumIndex equi = new EquilibriumIndex();
int arr[] = { -7, 1, 5, 2, -4, 3, 0 };
int arr_size = arr.length;
System.out.println(equi.equilibrium(arr, arr_size));
}
}
|
Python3
def equilibrium(arr):
leftsum = 0
rightsum = 0
n = len(arr)
for i in range(n):
leftsum = 0
rightsum = 0
for j in range(i):
leftsum += arr[j]
for j in range(i + 1, n):
rightsum += arr[j]
if leftsum == rightsum:
return i
return -1
if __name__ == "__main__":
arr = [-7, 1, 5, 2, -4, 3, 0]
print(equilibrium(arr))
|
C#
using System;
class GFG {
static int equilibrium(int[] arr, int n)
{
int i, j;
int leftsum, rightsum;
for (i = 0; i < n; ++i) {
leftsum = 0;
rightsum = 0;
for (j = 0; j < i; j++)
leftsum += arr[j];
for (j = i + 1; j < n; j++)
rightsum += arr[j];
if (leftsum == rightsum)
return i;
}
return -1;
}
public static void Main()
{
int[] arr = { -7, 1, 5, 2, -4, 3, 0 };
int arr_size = arr.Length;
Console.Write(equilibrium(arr, arr_size));
}
}
|
PHP
<?php
function equilibrium($arr, $n)
{
$i; $j;
$leftsum;
$rightsum;
for ($i = 0; $i < $n; ++$i)
{
$leftsum = 0;
for ($j = 0; $j < $i; $j++)
$leftsum += $arr[$j];
$rightsum = 0;
for ($j = $i + 1; $j < $n; $j++)
$rightsum += $arr[$j];
if ($leftsum == $rightsum)
return $i;
}
return -1;
}
$arr = array( -7, 1, 5, 2, -4, 3, 0 );
$arr_size = sizeof($arr);
echo equilibrium($arr, $arr_size);
?>
|
Javascript
<script>
function equilibrium(arr, n)
{
var i, j;
var leftsum, rightsum;
for(i = 0; i < n; ++i)
{
leftsum = 0;
for(let j = 0; j < i; j++)
leftsum += arr[j];
rightsum = 0;
for(let j = i + 1; j < n; j++)
rightsum += arr[j];
if(leftsum == rightsum)
return i;
}
return -1;
}
var arr = new Array(-7,1,5,2,-4,3,0);
n = arr.length;
document.write(equilibrium(arr,n));
</script>
|
Time Complexity: O(N2)
Auxiliary Space: O(1)
Equilibrium index of an Array using Array-Sum:
To solve the problem follow the below idea:
The idea is to get the total sum of the array first. Then Iterate through the array and keep updating the left sum which is initialized as zero. In the loop, we can get the right sum by subtracting the elements one by one. Thanks to Sambasiva for suggesting this solution and providing code for this.
Follow the given steps to solve the problem:
- Initialize leftsum as 0
- Get the total sum of the array as sum
- Iterate through the array and for each index i, do the following:
- Update the sum to get the right sum.
- sum = sum – arr[i]
- The sum is now the right sum
- If leftsum is equal to the sum, then return the current index.
- update left sum for the next iteration.
- leftsum = leftsum + arr[i]
- Return -1
- If we come out of the loop without returning then there is no equilibrium index
The image below shows the dry run of the above approach:
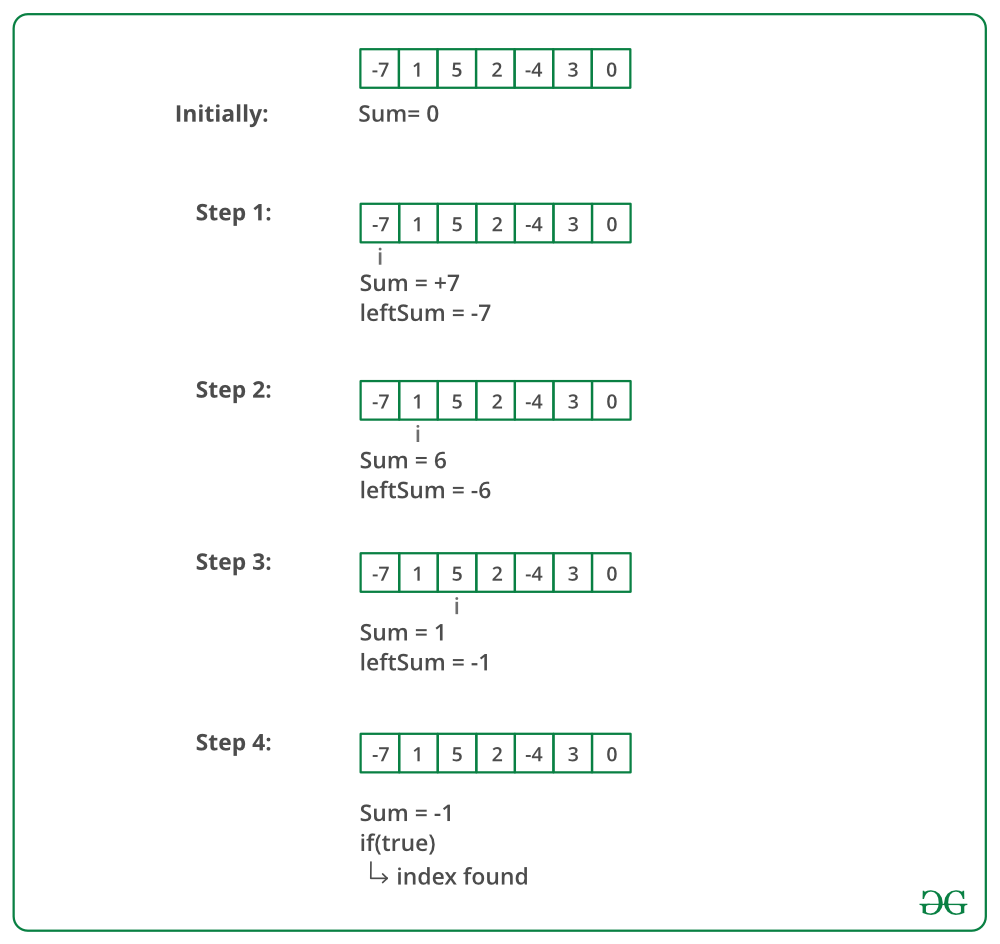
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int equilibrium(int arr[], int n)
{
int sum = 0;
int leftsum = 0;
for (int i = 0; i < n; ++i)
sum += arr[i];
for (int i = 0; i < n; ++i) {
sum -= arr[i];
if (leftsum == sum)
return i;
leftsum += arr[i];
}
return -1;
}
int main()
{
int arr[] = { -7, 1, 5, 2, -4, 3, 0 };
int arr_size = sizeof(arr) / sizeof(arr[0]);
cout << "First equilibrium index is "
<< equilibrium(arr, arr_size);
return 0;
}
|
C
#include <stdio.h>
int equilibrium(int arr[], int n)
{
int sum = 0;
int leftsum = 0;
for (int i = 0; i < n; ++i)
sum += arr[i];
for (int i = 0; i < n; ++i) {
sum -= arr[i];
if (leftsum == sum)
return i;
leftsum += arr[i];
}
return -1;
}
int main()
{
int arr[] = { -7, 1, 5, 2, -4, 3, 0 };
int arr_size = sizeof(arr) / sizeof(arr[0]);
printf("First equilibrium index is %d",
equilibrium(arr, arr_size));
getchar();
return 0;
}
|
Java
class EquilibriumIndex {
int equilibrium(int arr[], int n)
{
int sum = 0;
int leftsum = 0;
for (int i = 0; i < n; ++i)
sum += arr[i];
for (int i = 0; i < n; ++i) {
sum -= arr[i];
if (leftsum == sum)
return i;
leftsum += arr[i];
}
return -1;
}
public static void main(String[] args)
{
EquilibriumIndex equi = new EquilibriumIndex();
int arr[] = { -7, 1, 5, 2, -4, 3, 0 };
int arr_size = arr.length;
System.out.println(
"First equilibrium index is "
+ equi.equilibrium(arr, arr_size));
}
}
|
Python3
def equilibrium(arr):
total_sum = sum(arr)
leftsum = 0
for i, num in enumerate(arr):
total_sum -= num
if leftsum == total_sum:
return i
leftsum += num
return -1
if __name__ == "__main__":
arr = [-7, 1, 5, 2, -4, 3, 0]
print('First equilibrium index is ',
equilibrium(arr))
|
C#
using System;
class GFG {
static int equilibrium(int[] arr, int n)
{
int sum = 0;
int leftsum = 0;
for (int i = 0; i < n; ++i)
sum += arr[i];
for (int i = 0; i < n; ++i) {
sum -= arr[i];
if (leftsum == sum)
return i;
leftsum += arr[i];
}
return -1;
}
public static void Main()
{
int[] arr = { -7, 1, 5, 2, -4, 3, 0 };
int arr_size = arr.Length;
Console.Write("First equilibrium index is "
+ equilibrium(arr, arr_size));
}
}
|
PHP
<?php
function equilibrium($arr, $n)
{
$sum = 0;
$leftsum = 0;
for ($i = 0; $i < $n; ++$i)
$sum += $arr[$i];
for ($i = 0; $i < $n; ++$i)
{
$sum -= $arr[$i];
if ($leftsum == $sum)
return $i;
$leftsum += $arr[$i];
}
return -1;
}
$arr = array( -7, 1, 5, 2, -4, 3, 0 );
$arr_size = sizeof($arr);
echo "First equilibrium index is ",
equilibrium($arr, $arr_size);
?>
|
Javascript
<script>
function equilibrium(arr, n)
{
sum = 0;
leftsum = 0;
for (let i = 0; i < n; ++i)
sum += arr[i];
for (let i = 0; i < n; ++i)
{
sum -= arr[i];
if (leftsum == sum)
return i;
leftsum += arr[i];
}
return -1;
}
arr =new Array(-7, 1, 5, 2, -4, 3, 0);
n=arr.length;
document.write("First equilibrium index is " + equilibrium(arr, n));
</script>
|
Output
First equilibrium index is 3
Time Complexity: O(N)
Auxiliary Space: O(1)
Equilibrium index of an array using Prefix-Sum:
To solve the problem follow the below idea:
This is a quite simple and straightforward method. The idea is to take the prefix sum of the array twice. Once from the front end of the array and another from the back end of the array. After taking both prefix sums run a loop and check for some i if both the prefix sum from one array is equal to prefix sum from the second array then that point can be considered as the Equilibrium point
Follow the given steps to solve the problem:
- Declare two arrays to store the prefix sum of the array from the front and the back
- Run a loop from 1 to N and check if at any point prefix sum of the array from the front is equal to the prefix sum of the array from the back
- If any such index is found then return that index
- Else return -1
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int equilibrium(int a[], int n)
{
if (n == 1)
return (0);
int forward[n] = { 0 };
int rev[n] = { 0 };
forward[0]=a[0];
rev[n-1]=a[n-1];
for (int i = 1; i < n; i++) {
forward[i] = forward[i - 1] + a[i];
}
for (int i = n - 2; i >= 0; i--) {
rev[i] = rev[i + 1] + a[i];
}
for (int i = 0; i < n; i++) {
if (forward[i] == rev[i]) {
return i;
}
}
return -1;
}
int main()
{
int arr[] = { -7, 1, 5, 2, -4, 3, 0 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << "First Point of equilibrium is at index "
<< equilibrium(arr, n) << "\n";
return 0;
}
|
Java
import java.io.*;
class GFG {
static int equilibrium(int a[], int n)
{
if (n == 1)
return (0);
int[] front = new int[n];
int[] back = new int[n];
for (int i = 0; i < n; i++) {
if (i != 0) {
front[i] = front[i - 1] + a[i];
}
else {
front[i] = a[i];
}
}
for (int i = n - 1; i > 0; i--) {
if (i <= n - 2) {
back[i] = back[i + 1] + a[i];
}
else {
back[i] = a[i];
}
}
for (int i = 0; i < n; i++) {
if (front[i] == back[i]) {
return i;
}
}
return -1;
}
public static void main(String[] args)
{
int arr[] = { -7, 1, 5, 2, -4, 3, 0 };
int arr_size = arr.length;
System.out.println("First Point of equilibrium "
+ "is at index "
+ equilibrium(arr, arr_size));
}
}
|
Python3
def equilibrium(arr):
left_sum = []
right_sum = []
for i in range(len(arr)):
if(i):
left_sum.append(left_sum[i-1]+arr[i])
right_sum.append(right_sum[i-1]+arr[len(arr)-1-i])
else:
left_sum.append(arr[i])
right_sum.append(arr[len(arr)-1])
for i in range(len(arr)):
if(left_sum[i] == right_sum[len(arr) - 1 - i]):
return(i)
return -1
if __name__ == "__main__":
arr = [-7, 1, 5, 2, -4, 3, 0]
print('First equilibrium index is ',
equilibrium(arr))
|
C#
using System;
class GFG {
static int equilibrium(int[] a, int n)
{
if (n == 1)
return (0);
int[] front = new int[n];
int[] back = new int[n];
for (int i = 0; i < n; i++) {
if (i != 0) {
front[i] = front[i - 1] + a[i];
}
else {
front[i] = a[i];
}
}
for (int i = n - 1; i > 0; i--) {
if (i <= n - 2) {
back[i] = back[i + 1] + a[i];
}
else {
back[i] = a[i];
}
}
for (int i = 0; i < n; i++) {
if (front[i] == back[i]) {
return i;
}
}
return -1;
}
public static void Main(string[] args)
{
int[] arr = { -7, 1, 5, 2, -4, 3, 0 };
int arr_size = arr.Length;
Console.WriteLine("First Point of equilibrium "
+ "is at index "
+ equilibrium(arr, arr_size));
}
}
|
Javascript
<script>
function equilibrium(a, n)
{
if (n == 1)
return (0);
var forward = new Array(0);
var rev = new Array(0);
for (let i = 0; i < n; i++) {
if (i) {
forward[i] = forward[i - 1] + a[i];
}
else {
forward[i] = a[i];
}
}
for (let i = n - 1; i > 0; i--) {
if (i <= n - 2) {
rev[i] = rev[i + 1] + a[i];
}
else {
rev[i] = a[i];
}
}
for (let i = 0; i < n; i++) {
if (forward[i] == rev[i]) {
return i;
}
}
return -1;
}
arr = new Array(-7, 1, 5, 2, -4, 3, 0);
n = arr.length;
document.write("First Point of equilibrium is at index "
+ equilibrium(arr, n) + "\n");
</script>
|
Output
First Point of equilibrium is at index 3
Time Complexity: O(N)
Auxiliary Space: O(N)
Equilibrium index of an array using two pointers:
The given code is trying to find the equilibrium index of an array, where an equilibrium index is an index such that the sum of elements at lower indexes is equal to the sum of elements at higher indexes.
The code uses two pointers, left and right, to keep track of the sum of elements to the left and right of the pivot index. It starts by initializing the left pointer to 0, pivot to 0, and right pointer to the sum of all elements in the array minus the first element.
The code then enters a while loop where the pivot index is incremented until the left and right pointers are equal, or until the pivot index is the last index in the array.
In each iteration of the loop, the pivot index is incremented, and the right pointer is decremented by the value of the element at the current pivot index. The left pointer is incremented by the value of the element at the previous pivot index.
The code then checks if the left pointer is equal to the right pointer. If it is, the current pivot index is returned as the equilibrium index. If the pivot index is the last index in the array and the left pointer is still not equal to the right pointer, the function returns -1, indicating that no equilibrium index was found.
C++
#include <iostream>
#include <vector>
using namespace std;
int pivotIndex(vector<int>& nums) {
int left = 0, pivot = 0, right = 0;
for (int i = 1; i < nums.size(); i++) {
right += nums[i];
}
while (pivot < nums.size() - 1 && right != left) {
pivot++;
right -= nums[pivot];
left += nums[pivot - 1];
}
return (left == right) ? pivot : -1;
}
int main() {
vector<int> nums = {1, 7, 3, 6, 5, 6};
int result = pivotIndex(nums);
cout <<"First Point of equilibrium is at index "<< result << endl;
return 0;
}
|
Java
import java.util.List;
class Solution {
public int pivotIndex(List<Integer> nums) {
int left = 0, pivot = 0, right = 0;
for (int i = 1; i < nums.size(); i++) {
right += nums.get(i);
}
while (pivot < nums.size() - 1 && right != left) {
pivot++;
right -= nums.get(pivot);
left += nums.get(pivot - 1);
}
return (left == right) ? pivot : -1;
}
public static void main(String[] args) {
List<Integer> nums = List.of(1, 7, 3, 6, 5, 6);
int result = new Solution().pivotIndex(nums);
System.out.println(result);
}
}
|
Python3
from typing import List
def pivotIndex(nums: List[int]) -> int:
left, pivot, right = 0, 0, sum(nums)-nums[0]
while pivot < len(nums)-1 and right != left:
pivot += 1
right -= nums[pivot]
left += nums[pivot-1]
return pivot if left == right else -1
def main():
nums = [1, 7, 3, 6, 5, 6]
result = pivotIndex(nums)
print(result)
if __name__ == "__main__":
main()
|
Javascript
function pivotIndex(nums) {
let left = 0, pivot = 0, right = nums.slice(1).reduce((a, b) => a + b, 0);
while (pivot < nums.length - 1 && right !== left) {
pivot++;
right -= nums[pivot];
left += nums[pivot - 1];
}
return (left === right) ? pivot : -1;
}
console.log(pivotIndex([1, 7, 3, 6, 5, 6]));
|
C#
using System;
using System.Linq;
class Solution {
public static int PivotIndex(int[] nums) {
int left = 0, pivot = 0, right = nums.Skip(1).Sum();
while (pivot < nums.Length - 1 && right != left) {
pivot++;
right -= nums[pivot];
left += nums[pivot - 1];
}
return (left == right) ? pivot : -1;
}
public static void Main(string[] args) {
int[] nums = {1, 7, 3, 6, 5, 6};
int result = PivotIndex(nums);
Console.WriteLine(result);
}
}
|
Output
First Point of equilibrium is at index 3
Time Complexity: O(N)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...