Linked List representation of Disjoint Set Data Structures

Last Updated : 15 Sep, 2023

Prerequisites : Union Find (or Disjoint Set), Disjoint Set Data Structures (Java Implementation)

A disjoint-set data structure maintains a collection S = {S₁, S₂,…., S_k} of disjoint dynamic sets. We identify each set by a representative, which is some member of the set. In some applications, it doesn’t matter which member is used as the representative; we care only that if we ask for the representative of a dynamic set twice without modifying the set between the requests, we get the same answer both times. Other applications may require a prespecified rule for choosing the representative, such as choosing the smallest member in the set.

Example: Determining the connected components of an undirected graph. Below figure, shows a graph with four connected components.

Fig (a)

Solution : One procedure X that follows uses the disjoint-set operations to compute the connected components of a graph. Once X has pre-processed the graph, the procedure Y answers queries about whether two vertices are in the same connected component. Below figure shows the collection of disjoint sets after processing each edge.

Fig (b)

See here as the above example was discussed earlier.
Fig 2

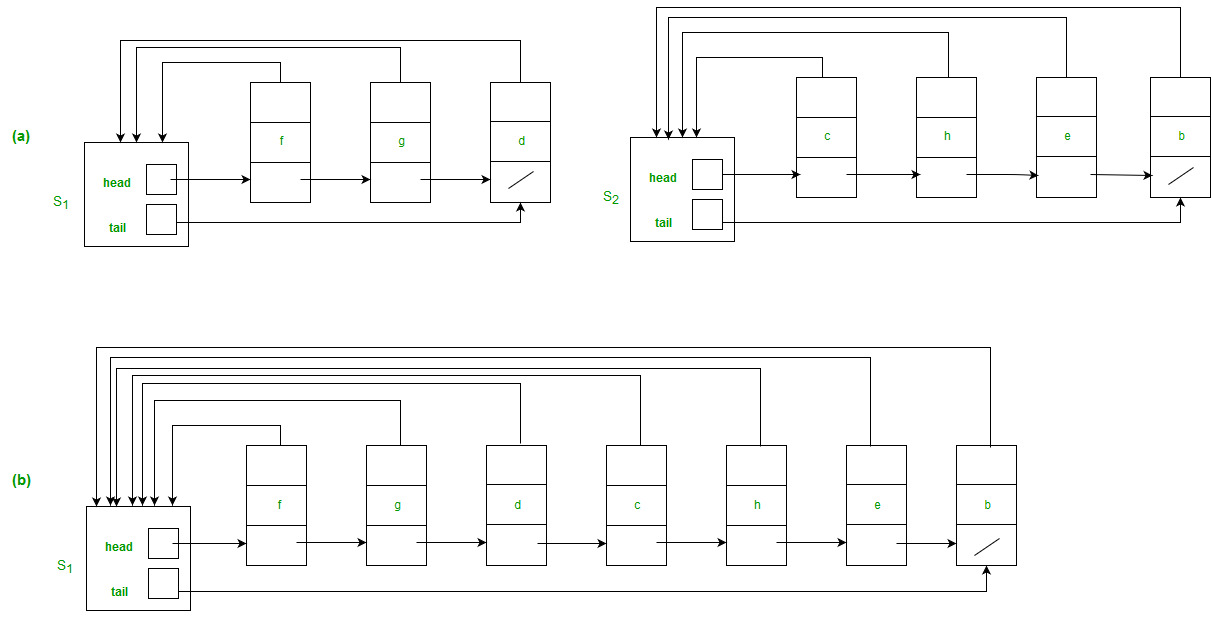
Figure

(a) Linked-list representations of two sets. Set S1 contains members d, f, and g, with representative f, and set S2 contains members b, c, e, and h, with representative c.
Each object in the list contains a set member, a pointer to the next object in the list, and a pointer back to the set object. Each set object has pointers head and tail to the first and last objects, respectively.

b) The result of UNION(e, g), which appends the linked list containing e to the linked list containing g. The representative of the resulting set is f . The set object for e’s list, S2, is destroyed.
Above three figures are taken from the Cormen(CLRS) book. Above Figure shows a simple way to implement a disjoint-set data structure: each set is represented by its own linked list. The object for each set has attributes head, pointing to the 1st object in the list, and tail, pointing to the last object.
Each object in the list contains a set member, a pointer to the next object in the list, and a pointer back to the set object. Within each linked list, the objects may appear in any order. The representative is the set member in the 1st object in the list. To carry out MAKE-SET (x), we create a new linked list whose only object is x. For FIND-SET(x), we just follow the pointer from x back to its set object and then return the member in the object that head points to. For example, in the Figure, the call FIND-SET(g) would return f.

Algorithm:

Letting x denote an object, we wish to support the following operations:

MAKE-SET(x) creates a new set whose only member (and thus representative) is x. Since the sets are disjoint, we require that x not already be in some other set.

UNION (x, y) unites the dynamic sets that contain x and y, say S_x and S_y, into a new set that is the union of these two sets. We assume that the two sets are disjoint prior to the operation. The representative of the resulting set is any member of S_x U S_y, although many implementations of UNION specifically choose the representative of either S_x or S_y as the new representative. Since we require the sets in the collection to be disjoint, conceptually we destroy sets S_x and S_y, removing them from the collection S. In practice, we often absorb the elements of one of the sets into the other set.

FIND-SET(x) returns a pointer to the representative of the (unique) set containing x.

Based on the above explanation, below are implementations:

CPP

// C++ program for implementation of disjoint
// set data structure using linked list
#include <bits/stdc++.h>
using namespace std;
 
// to represent linked list which is a set
struct Item;
 
// to represent Node of linked list. Every
// node has a pointer to representative
struct Node
{
    int val;
    Node *next;
    Item *itemPtr;
};
 
// A list has a pointer to head and tail
struct Item
{
    Node *hd, *tl;
};
 
// To represent union set
class ListSet
{
private:
 
    // Hash to store addresses of set representatives
    // for given values. It is made global for ease of
    // implementation. And second part of hash is actually
    // address of Nodes. We typecast addresses to long
    // before storing them.
    unordered_map<int, Node *> nodeAddress;
 
public:
    void makeset(int a);
    Item* find(int key);
    void Union(Item *i1, Item *i2);
};
 
// To make a set with one object
// with its representative
void ListSet::makeset(int a)
{
    // Create a new Set
    Item *newSet = new Item;
 
    // Create a new linked list node
    // to store given key
    newSet->hd = new Node;
 
    // Initialize head and tail
    newSet->tl = newSet->hd;
    nodeAddress[a] = newSet->hd;
 
    // Create a new set
    newSet->hd->val = a;
    newSet->hd->itemPtr = newSet;
    newSet->hd->next = NULL;
}
 
// To find representative address of a
// key
Item *ListSet::find(int key)
{
    Node *ptr = nodeAddress[key];
    return (ptr->itemPtr);
}
 
// union function for joining two subsets
// of a universe. Merges set2 into set1
// and deletes set1.
void ListSet::Union(Item *set1, Item *set2)
{
    Node *cur = set2->hd;
    while (cur != 0)
    {
        cur->itemPtr = set1;
        cur = cur->next;
    }
 
    // Join the tail of the set to head
    // of the input set
    (set1->tl)->next = set2->hd;
    set1->tl = set2->tl;
 
    delete set2;
}
 
// Driver code
int main()
{
    ListSet a;
    a.makeset(13); //a new set is made with one object only
    a.makeset(25);
    a.makeset(45);
    a.makeset(65);
 
    cout << "find(13): " << a.find(13) << endl;
    cout << "find(25): "
        << a.find(25) << endl;
    cout << "find(65): "
        << a.find(65) << endl;
    cout << "find(45): "
        << a.find(45) << endl << endl;
    cout << "Union(find(65), find(45)) \n";
 
    a.Union(a.find(65), a.find(45));
 
    cout << "find(65]): "
        << a.find(65) << endl;
    cout << "find(45]): "
        << a.find(45) << endl;
    return 0;
}

Java

// Java program for implementation of disjoint
// set data structure using linked list
import java.util.*;
 
// to represent Node of linked list. Every
// node has a pointer to representative
class Node {
    int val;
    Node next;
    Item itemPtr;
}
 
// A list has a pointer to head and tail
class Item {
    Node hd, tl;
}
 
// To represent union set
public class ListSet {
 
    // Hash to store addresses of set representatives
    // for given values. It is made global for ease of
    // implementation. And second part of hash is actually
    // address of Nodes. We typecast addresses to long
    // before storing them.
    private Map<Integer, Node> nodeAddress
        = new HashMap<>();
 
    // To make a set with one object
    // with its representative
    public void makeset(int a)
    {
        // Create a new Set
        Item newSet = new Item();
 
        // Create a new linked list node
        // to store given key
        newSet.hd = new Node();
 
        // Initialize head and tail
        newSet.tl = newSet.hd;
        nodeAddress.put(a, newSet.hd);
 
        // Create a new set
        newSet.hd.val = a;
        newSet.hd.itemPtr = newSet;
        newSet.hd.next = null;
    }
 
    // To find representative address of a
    // key
    public Item find(int key)
    {
        Node ptr = nodeAddress.get(key);
        return ptr.itemPtr;
    }
 
    // union function for joining two subsets
    // of a universe. Merges set2 into set1
    // and deletes set1.
    public void Union(Item set1, Item set2)
    {
        Node cur = set2.hd;
        while (cur != null) {
            cur.itemPtr = set1;
            cur = cur.next;
        }
 
        // Join the tail of the set to head
        // of the input set
        set1.tl.next = set2.hd;
        set1.tl = set2.tl;
        set2 = null;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        ListSet a = new ListSet();
        a.makeset(13);
        a.makeset(25);
        a.makeset(45);
        a.makeset(65);
 
        System.out.println("find(13): " + a.find(13).hashCode());
        System.out.println("find(25): " + a.find(25).hashCode());
        System.out.println("find(65): " + a.find(65).hashCode());
        System.out.println("find(45): " + a.find(45).hashCode()
                           + "\n");
        System.out.println("Union(find(65), find(45))");
 
        a.Union(a.find(65), a.find(45));
 
        System.out.println("find(65): " + a.find(65).hashCode());
        System.out.println("find(45): " + a.find(45).hashCode());
    }
}

Python3

from collections import defaultdict
 
class Node:
    def __init__(self, val, item_ptr):
        self.val = val
        self.item_ptr = item_ptr
        self.next = None
 
class Item:
    def __init__(self, hd, tl):
        self.hd = hd
        self.tl = tl
 
class ListSet:
    def __init__(self):
        self.node_address = defaultdict(lambda: None)
 
    def makeset(self, a):
        new_set = Item(Node(a, None), None)
        new_set.hd.item_ptr = new_set
        new_set.tl = new_set.hd
        self.node_address[a] = new_set.hd
 
    def find(self, key):
        node = self.node_address[key]
        return node.item_ptr
 
    def union(self, i1, i2):
        cur = i2.hd
        while cur:
            cur.item_ptr = i1
            cur = cur.next
        i1.tl.next = i2.hd
        i1.tl = i2.tl
        del i2
 
def main():
    a = ListSet()
    a.makeset(13)
    a.makeset(25)
    a.makeset(45)
    a.makeset(65)
 
    print(f"find(13): {a.find(13)}")
    print(f"find(25): {a.find(25)}")
    print(f"find(65): {a.find(65)}")
    print(f"find(45): {a.find(45)}")
    print()
    print("Union(find(65), find(45))")
    a.union(a.find(65), a.find(45))
    print(f"find(65): {a.find(65)}")
    print(f"find(45): {a.find(45)}")
 
if __name__ == "__main__":
    main()

C#

// C# program for implementation of disjoint
// set data structure using linked list
using System;
using System.Collections.Generic;
 
class Program {
    // Driver Code
    static void Main(string[] args)
    {
        ListSet a = new ListSet();
        a.makeset(13);
        a.makeset(25);
        a.makeset(45);
        a.makeset(65);
 
        Console.WriteLine("find(13): "
                          + a.find(13).GetHashCode());
        Console.WriteLine("find(25): "
                          + a.find(25).GetHashCode());
        Console.WriteLine("find(65): "
                          + a.find(65).GetHashCode());
        Console.WriteLine(
            "find(45): " + a.find(45).GetHashCode() + "\n");
        Console.WriteLine("Union(find(65), find(45))");
 
        a.Union(a.find(65), a.find(45));
 
        Console.WriteLine("find(65): "
                          + a.find(65).GetHashCode());
        Console.WriteLine("find(45): "
                          + a.find(45).GetHashCode());
    }
}
 
// to represent Node of linked list. Every
// node has a pointer to representative
class Node {
    public int val;
    public Node next;
    public Item itemPtr;
}
 
// A list has a pointer to head and tail
class Item {
    public Node hd, tl;
}
 
// To represent union set
class ListSet {
 
    // Hash to store addresses of set representatives
    // for given values. It is made global for ease of
    // implementation. And second part of hash is actually
    // address of Nodes. We typecast addresses to long
    // before storing them.
    private Dictionary<int, Node> nodeAddress
        = new Dictionary<int, Node>();
 
    // To make a set with one object
    // with its representative
    public void makeset(int a)
    {
        // Create a new Set
        Item newSet = new Item();
 
        // Create a new linked list node
        // to store given key
        newSet.hd = new Node();
 
        // Initialize head and tail
        newSet.tl = newSet.hd;
        nodeAddress.Add(a, newSet.hd);
 
        // Create a new set
        newSet.hd.val = a;
        newSet.hd.itemPtr = newSet;
        newSet.hd.next = null;
    }
 
    // To find representative address of a
    // key
    public Item find(int key)
    {
        Node ptr = nodeAddress[key];
        return ptr.itemPtr;
    }
 
    // union function for joining two subsets
    // of a universe. Merges set2 into set1
    // and deletes set1.
    public void Union(Item set1, Item set2)
    {
        Node cur = set2.hd;
        while (cur != null) {
            cur.itemPtr = set1;
            cur = cur.next;
        }
 
        // Join the tail of the set to head
        // of the input set
        set1.tl.next = set2.hd;
        set1.tl = set2.tl;
        set2 = null;
    }
}
 
// This code is contributed by Tapesh(tapeshdua420)

Javascript

// To represent linked list which is a set
class Item {
    constructor() {
        this.hd = null;
        this.tl = null;
    }
}
 
// To represent Node of linked list. Every
// node has a pointer to representative
class Node {
    constructor(val) {
        this.val = val;
        this.next = null;
        this.itemPtr = null;
    }
}
 
// To represent union set
class ListSet {
    constructor() {
        this.nodeAddress = new Map();
    }
 
    makeset(a) {
        // Create a new Set
        const newSet = new Item();
 
        // Create a new linked list node
        // to store the given key
        newSet.hd = new Node(a);
 
        // Initialize head and tail
        newSet.tl = newSet.hd;
        this.nodeAddress.set(a, newSet.hd);
 
        // Create a new set
        newSet.hd.itemPtr = newSet;
        newSet.hd.next = null;
    }
 
    find(key) {
        const ptr = this.nodeAddress.get(key);
        return ptr ? ptr.itemPtr : null;
    }
 
    Union(set1, set2) {
        let cur = set2.hd;
        while (cur !== null) {
            cur.itemPtr = set1;
            cur = cur.next;
        }
 
        // Join the tail of the set to the head
        // of the input set
        set1.tl.next = set2.hd;
        set1.tl = set2.tl;
 
        set2.hd = null;
        set2.tl = null;
    }
}
 
// Driver code
const a = new ListSet();
a.makeset(13);
a.makeset(25);
a.makeset(45);
a.makeset(65);
 
console.log("find(13):", a.find(13));
console.log("find(25):", a.find(25));
console.log("find(65):", a.find(65));
console.log("find(45):", a.find(45));
console.log("\nUnion(find(65), find(45))");
 
a.Union(a.find(65), a.find(45));
 
console.log("find(65):", a.find(65));
console.log("find(45):", a.find(45));

Output

find(13): 0x1cf8c20
find(25): 0x1cf8ca0
find(65): 0x1cf8d70
find(45): 0x1cf8c80

Union(find(65), find(45)) 
find(65]): 0x1cf8d70
find(45]): 0x1cf8d70

Note: The node address will change every time, we run the program. Time complexities of MAKE-SET and FIND-SET are O(1). Time complexity for UNION is O(n).

Suggest improvement

Delete a given node in Linked List under given constraints

Perfect cubes in a range

Share your thoughts in the comments

Linked List representation of Disjoint Set Data Structures

CPP

Java

Python3

C#

Javascript

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?