Evaluation of Postfix Expression

Last Updated : 27 Mar, 2023

Given a postfix expression, the task is to evaluate the postfix expression.

Postfix expression: The expression of the form “a b operator” (ab+) i.e., when a pair of operands is followed by an operator.

Examples:

Input: str = “2 3 1 * + 9 -“
Output: -4
Explanation: If the expression is converted into an infix expression, it will be 2 + (3 * 1) – 9 = 5 – 9 = -4.

Input: str = “100 200 + 2 / 5 * 7 +”
Output: 757

Evaluation of Postfix Expression using Stack:

To evaluate a postfix expression we can use a stack.

Iterate the expression from left to right and keep on storing the operands into a stack. Once an operator is received, pop the two topmost elements and evaluate them and push the result in the stack again.

Illustration:

Follow the below illustration for a better understanding:

Consider the expression: exp = “2 3 1 * + 9 -“

Scan 2, it’s a number, So push it into stack. Stack contains ‘2’.

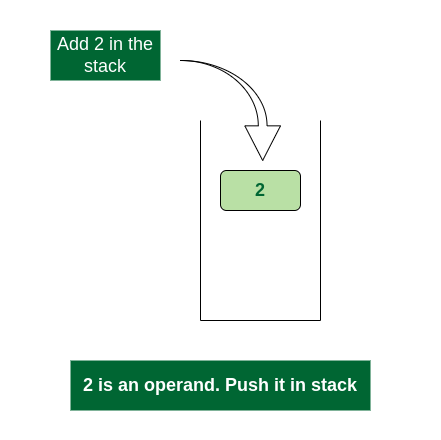
Push 2 into stack

Scan 3, again a number, push it to stack, stack now contains ‘2 3’ (from bottom to top)

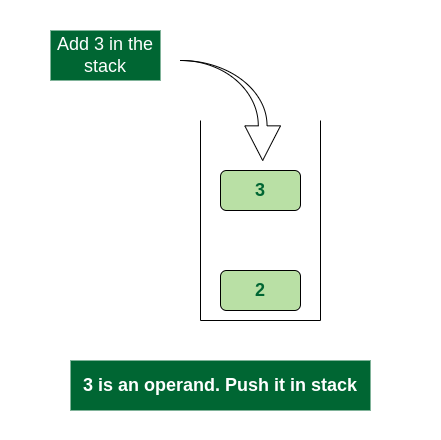
Push 3 into stack

Scan 1, again a number, push it to stack, stack now contains ‘2 3 1’

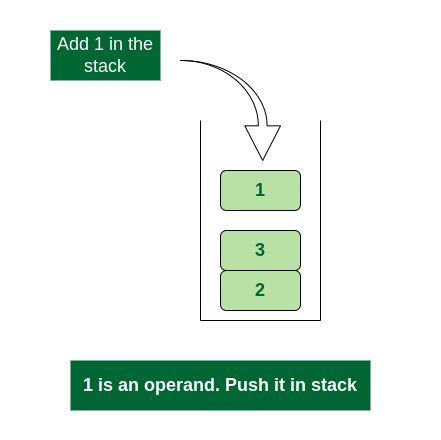
Push 1 into stack

Scan *, it’s an operator. Pop two operands from stack, apply the * operator on operands. We get 3*1 which results in 3. We push the result 3 to stack. The stack now becomes ‘2 3’.

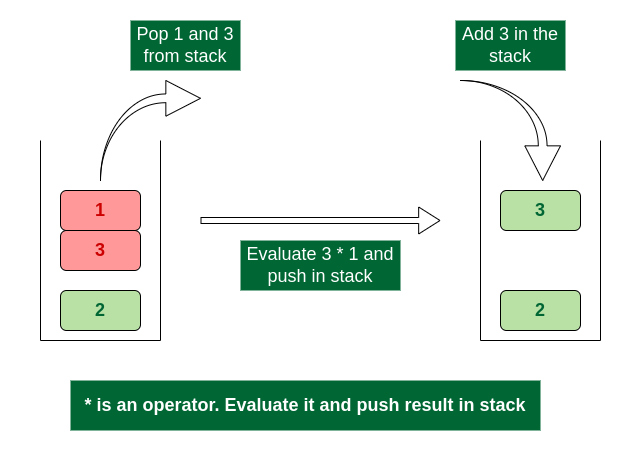
Evaluate * operator and push result in stack

Scan +, it’s an operator. Pop two operands from stack, apply the + operator on operands. We get 3 + 2 which results in 5. We push the result 5 to stack. The stack now becomes ‘5’.

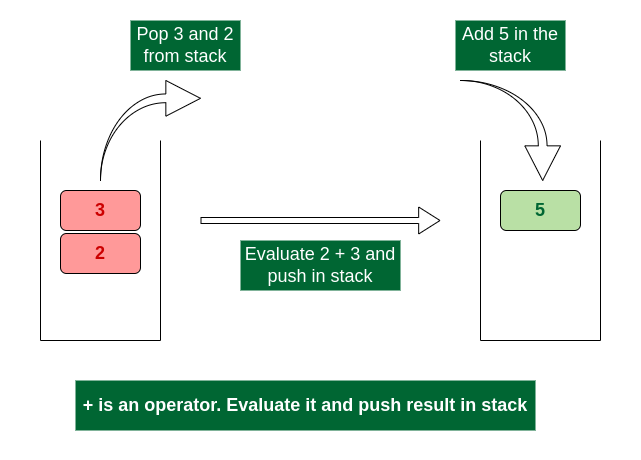
Evaluate + operator and push result in stack

Scan 9, it’s a number. So we push it to the stack. The stack now becomes ‘5 9’.

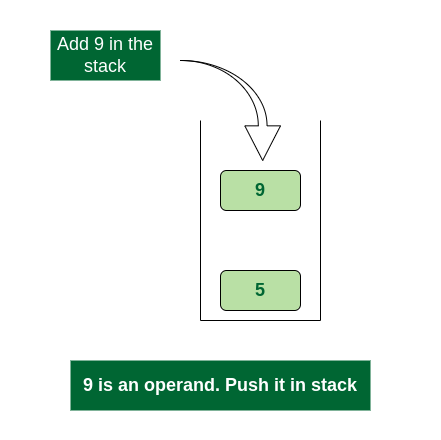
Push 9 into stack

Scan -, it’s an operator, pop two operands from stack, apply the – operator on operands, we get 5 – 9 which results in -4. We push the result -4 to the stack. The stack now becomes ‘-4’.

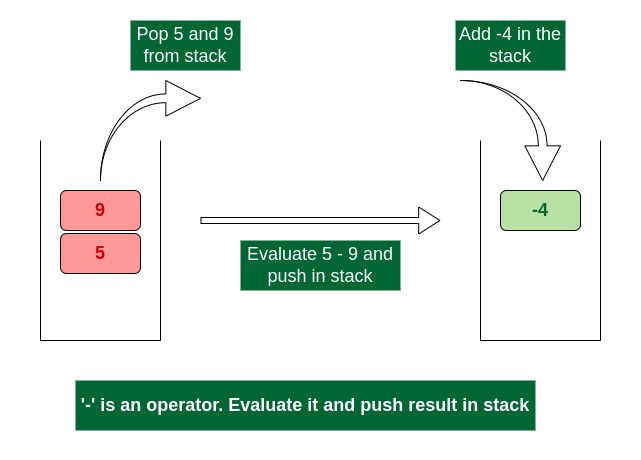
Evaluate ‘-‘ operator and push result in stack

There are no more elements to scan, we return the top element from the stack (which is the only element left in a stack).

So the result becomes -4.

Follow the steps mentioned below to evaluate postfix expression using stack:

Create a stack to store operands (or values).
Scan the given expression from left to right and do the following for every scanned element.
- If the element is a number, push it into the stack.
- If the element is an operator, pop operands for the operator from the stack. Evaluate the operator and push the result back to the stack.
When the expression is ended, the number in the stack is the final answer.

Below is the implementation of the above approach:

C

// C program to evaluate value of a postfix expression
#include <ctype.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
 
// Stack type
struct Stack {
    int top;
    unsigned capacity;
    int* array;
};
 
// Stack Operations
struct Stack* createStack(unsigned capacity)
{
    struct Stack* stack
        = (struct Stack*)malloc(sizeof(struct Stack));
 
    if (!stack)
        return NULL;
 
    stack->top = -1;
    stack->capacity = capacity;
    stack->array
        = (int*)malloc(stack->capacity * sizeof(int));
 
    if (!stack->array)
        return NULL;
 
    return stack;
}
 
int isEmpty(struct Stack* stack)
{
    return stack->top == -1;
}
 
char peek(struct Stack* stack)
{
    return stack->array[stack->top];
}
 
char pop(struct Stack* stack)
{
    if (!isEmpty(stack))
        return stack->array[stack->top--];
    return '$';
}
 
void push(struct Stack* stack, char op)
{
    stack->array[++stack->top] = op;
}
 
// The main function that returns value 
// of a given postfix expression
int evaluatePostfix(char* exp)
{
    // Create a stack of capacity equal to expression size
    struct Stack* stack = createStack(strlen(exp));
    int i;
 
    // See if stack was created successfully
    if (!stack)
        return -1;
 
    // Scan all characters one by one
    for (i = 0; exp[i]; ++i) {
         
        // If the scanned character is an operand 
        // (number here), push it to the stack.
        if (isdigit(exp[i]))
            push(stack, exp[i] - '0');
 
        // If the scanned character is an operator, 
        // pop two elements from stack apply the operator
        else {
            int val1 = pop(stack);
            int val2 = pop(stack);
            switch (exp[i]) {
            case '+':
                push(stack, val2 + val1);
                break;
            case '-':
                push(stack, val2 - val1);
                break;
            case '*':
                push(stack, val2 * val1);
                break;
            case '/':
                push(stack, val2 / val1);
                break;
            }
        }
    }
    return pop(stack);
}
 
// Driver code
int main()
{
    char exp[] = "231*+9-";
   
    // Function call
    printf("postfix evaluation: %d", evaluatePostfix(exp));
    return 0;
}

C++

// C++ program to evaluate value of a postfix expression
#include <bits/stdc++.h>
using namespace std;
 
// The main function that returns value 
// of a given postfix expression
int evaluatePostfix(string exp)
{
    // Create a stack of capacity equal to expression size
    stack<int> st;
 
    // Scan all characters one by one
    for (int i = 0; i < exp.size(); ++i) {
         
        // If the scanned character is an operand 
        // (number here), push it to the stack.
        if (isdigit(exp[i]))
            st.push(exp[i] - '0');
 
        // If the scanned character is an operator, 
        // pop two elements from stack apply the operator
        else {
            int val1 = st.top();
            st.pop();
            int val2 = st.top();
            st.pop();
            switch (exp[i]) {
            case '+':
                st.push(val2 + val1);
                break;
            case '-':
                st.push(val2 - val1);
                break;
            case '*':
                st.push(val2 * val1);
                break;
            case '/':
                st.push(val2 / val1);
                break;
            }
        }
    }
    return st.top();
}
 
// Driver code
int main()
{
    string exp = "231*+9-";
   
    // Function call
    cout << "postfix evaluation: " << evaluatePostfix(exp);
    return 0;
}

Java

// Java program to evaluate value of a postfix expression
 
import java.util.Stack;
 
public class Test {
     
    // Method to evaluate value of a postfix expression
    static int evaluatePostfix(String exp)
    {
        // Create a stack
        Stack<Integer> stack = new Stack<>();
 
        // Scan all characters one by one
        for (int i = 0; i < exp.length(); i++) {
            char c = exp.charAt(i);
 
            // If the scanned character is an operand
            // (number here), push it to the stack.
            if (Character.isDigit(c))
                stack.push(c - '0');
 
            //  If the scanned character is an operator, pop
            //  two elements from stack apply the operator
            else {
                int val1 = stack.pop();
                int val2 = stack.pop();
 
                switch (c) {
                case '+':
                    stack.push(val2 + val1);
                    break;
                case '-':
                    stack.push(val2 - val1);
                    break;
                case '/':
                    stack.push(val2 / val1);
                    break;
                case '*':
                    stack.push(val2 * val1);
                    break;
                }
            }
        }
        return stack.pop();
    }
 
    // Driver code
    public static void main(String[] args)
    {
        String exp = "231*+9-";
       
        // Function call
        System.out.println("postfix evaluation: "
                           + evaluatePostfix(exp));
    }
}
// Contributed by Sumit Ghosh

Python3

# Python program to evaluate value of a postfix expression
 
 
# Class to convert the expression
class Evaluate:
 
    # Constructor to initialize the class variables
    def __init__(self, capacity):
        self.top = -1
        self.capacity = capacity
         
        # This array is used a stack
        self.array = []
 
    # Check if the stack is empty
    def isEmpty(self):
        return True if self.top == -1 else False
 
    # Return the value of the top of the stack
    def peek(self):
        return self.array[-1]
 
    # Pop the element from the stack
    def pop(self):
        if not self.isEmpty():
            self.top -= 1
            return self.array.pop()
        else:
            return "$"
 
    # Push the element to the stack
    def push(self, op):
        self.top += 1
        self.array.append(op)
 
    # The main function that converts given infix expression
    # to postfix expression
    def evaluatePostfix(self, exp):
 
        # Iterate over the expression for conversion
        for i in exp:
 
            # If the scanned character is an operand
            # (number here) push it to the stack
            if i.isdigit():
                self.push(i)
 
            # If the scanned character is an operator,
            # pop two elements from stack and apply it.
            else:
                val1 = self.pop()
                val2 = self.pop()
                self.push(str(eval(val2 + i + val1)))
 
        return int(self.pop())
 
 
 
# Driver code
if __name__ == '__main__':
    exp = "231*+9-"
    obj = Evaluate(len(exp))
     
    # Function call
    print("postfix evaluation: %d" % (obj.evaluatePostfix(exp)))
 
     
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

C#

// C# program to evaluate value of a postfix expression
using System;
using System.Collections;
 
namespace GFG {
class Geek {
   
    // Main() method
    static void Main()
    {
        Geek e = new Geek();
        e.v = ("231*+9-");
        e.expression();
        Console.WriteLine("postfix evaluation: "
                          + e.answer);
        Console.Read();
    }
 
    //'v' is variable to store the string value
    public string v;
 
    public string answer;
    Stack i = new Stack();
 
    // evaluation method
    public void expression()
    {
        int a, b, ans;
        for (int j = 0; j < v.Length; j++)
        {
            String c = v.Substring(j, 1);
            if (c.Equals("*")) {
                String sa = (String)i.Pop();
                String sb = (String)i.Pop();
                a = Convert.ToInt32(sb);
                b = Convert.ToInt32(sa);
                ans = a * b;
                i.Push(ans.ToString());
            }
            else if (c.Equals("/")) {
                String sa = (String)i.Pop();
                String sb = (String)i.Pop();
                a = Convert.ToInt32(sb);
                b = Convert.ToInt32(sa);
                ans = a / b;
                i.Push(ans.ToString());
            }
            else if (c.Equals("+")) {
                String sa = (String)i.Pop();
                String sb = (String)i.Pop();
                a = Convert.ToInt32(sb);
                b = Convert.ToInt32(sa);
                ans = a + b;
                i.Push(ans.ToString());
            }
            else if (c.Equals("-")) {
                String sa = (String)i.Pop();
                String sb = (String)i.Pop();
                a = Convert.ToInt32(sb);
                b = Convert.ToInt32(sa);
                ans = a - b;
                i.Push(ans.ToString());
            }
            else {
                i.Push(v.Substring(j, 1));
            }
        }
        answer = (String)i.Pop();
    }
}
}

Javascript

<script>
 
// Javascript program to evaluate value of a postfix expression
 
// Method to evaluate value of a postfix expression
function evaluatePostfix(exp)
{
    //create a stack
        let stack=[];
          
        // Scan all characters one by one
        for(let i=0;i<exp.length;i++)
        {
            let c=exp[i];
              
            // If the scanned character is an operand (number here),
            // push it to the stack.
            if(! isNaN( parseInt(c) ))
            stack.push(c.charCodeAt(0) - '0'.charCodeAt(0));
              
            //  If the scanned character is an operator, pop two
            // elements from stack apply the operator
            else
            {
                let val1 = stack.pop();
                let val2 = stack.pop();
                  
                switch(c)
                {
                    case '+':
                    stack.push(val2+val1);
                    break;
                      
                    case '-':
                    stack.push(val2- val1);
                    break;
                      
                    case '/':
                    stack.push(val2/val1);
                    break;
                      
                    case '*':
                    stack.push(val2*val1);
                    break;
              }
            }
        }
        return stack.pop();   
}
 
// Driver program to test above functions
let exp="231*+9-";
document.write("postfix evaluation: "+evaluatePostfix(exp));
 
// This code is contributed by avanitrachhadiya2155
</script>

Output

postfix evaluation: -4

Time Complexity: O(N)
Auxiliary Space: O(N)

There are the following limitations of the above implementation.

It supports only 4 binary operators ‘+’, ‘*’, ‘-‘ and ‘/’. It can be extended for more operators by adding more switch cases.
The allowed operands are only single-digit operands.

Postfix evaluation for multi-digit numbers:

The above program can be extended for multiple digits by adding a separator-like space between all elements (operators and operands) of the given expression.

Below given is the extended program which allows operands to have multiple digits.

C

// C program to evaluate value of a postfix
// expression having multiple digit operands
#include <ctype.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
 
// Stack type
struct Stack {
    int top;
    unsigned capacity;
    int* array;
};
 
// Stack Operations
struct Stack* createStack(unsigned capacity)
{
    struct Stack* stack
        = (struct Stack*)malloc(sizeof(struct Stack));
 
    if (!stack)
        return NULL;
 
    stack->top = -1;
    stack->capacity = capacity;
    stack->array
        = (int*)malloc(stack->capacity * sizeof(int));
 
    if (!stack->array)
        return NULL;
 
    return stack;
}
 
int isEmpty(struct Stack* stack)
{
    return stack->top == -1;
}
 
int peek(struct Stack* stack)
{
    return stack->array[stack->top];
}
 
int pop(struct Stack* stack)
{
    if (!isEmpty(stack))
        return stack->array[stack->top--];
    return '$';
}
 
void push(struct Stack* stack, int op)
{
    stack->array[++stack->top] = op;
}
 
// The main function that returns value
// of a given postfix expression
int evaluatePostfix(char* exp)
{
    // Create a stack of capacity equal to expression size
    struct Stack* stack = createStack(strlen(exp));
    int i;
 
    // See if stack was created successfully
    if (!stack)
        return -1;
 
    // Scan all characters one by one
    for (i = 0; exp[i]; ++i) {
        // if the character is blank space then continue
        if (exp[i] == ' ')
            continue;
 
        // If the scanned character is an
        // operand (number here),extract the full number
        // Push it to the stack.
        else if (isdigit(exp[i])) {
            int num = 0;
 
            // extract full number
            while (isdigit(exp[i])) {
                num = num * 10 + (int)(exp[i] - '0');
                i++;
            }
            i--;
 
            // push the element in the stack
            push(stack, num);
        }
 
        // If the scanned character is an operator, pop two
        // elements from stack apply the operator
        else {
            int val1 = pop(stack);
            int val2 = pop(stack);
 
            switch (exp[i]) {
            case '+':
                push(stack, val2 + val1);
                break;
            case '-':
                push(stack, val2 - val1);
                break;
            case '*':
                push(stack, val2 * val1);
                break;
            case '/':
                push(stack, val2 / val1);
                break;
            }
        }
    }
    return pop(stack);
}
 
// Driver program to test above functions
int main()
{
    char exp[] = "100 200 + 2 / 5 * 7 +";
   
    // Function call
    printf("%d", evaluatePostfix(exp));
    return 0;
}
 
// This code is contributed by Arnab Kundu

C++14

// C++ program to evaluate value of a postfix
// expression having multiple digit operands
#include <bits/stdc++.h>
using namespace std;
 
// The main function that returns value
// of a given postfix expression
int evaluatePostfix(char* exp)
{
    // Create a stack of capacity equal to expression size
    stack<int> st;
    int i;
 
    // Scan all characters one by one
    for (i = 0; exp[i]; ++i) {
         
        // If the character is blank space then continue
        if (exp[i] == ' ')
            continue;
 
        // If the scanned character is an
        // operand (number here),extract the full number
        // Push it to the stack.
        else if (isdigit(exp[i])) {
            int num = 0;
 
            // Extract full number
            while (isdigit(exp[i])) {
                num = num * 10 + (int)(exp[i] - '0');
                i++;
            }
            i--;
 
            // Push the element in the stack
            st.push(num);
        }
 
        // If the scanned character is an operator, pop two
        // elements from stack apply the operator
        else {
            int val1 = st.top();
            st.pop();
            int val2 = st.top();
            st.pop();
 
            switch (exp[i]) {
            case '+':
                st.push(val2 + val1);
                break;
            case '-':
                st.push(val2 - val1);
                break;
            case '*':
                st.push(val2 * val1);
                break;
            case '/':
                st.push(val2 / val1);
                break;
            }
        }
    }
    return st.top();
}
 
// Driver code
int main()
{
    char exp[] = "100 200 + 2 / 5 * 7 +";
   
    // Function call
    cout << evaluatePostfix(exp);
    return 0;
}
 
// This code is contributed by rathbhupendra

Java

// Java program to evaluate value of a postfix
// expression having multiple digit operands
import java.util.Stack;
 
class Test1 {
     
    // Method to evaluate value of a postfix expression
    static int evaluatePostfix(String exp)
    {
        // Create a stack
        Stack<Integer> stack = new Stack<>();
 
        // Scan all characters one by one
        for (int i = 0; i < exp.length(); i++) {
            char c = exp.charAt(i);
 
            if (c == ' ')
                continue;
 
            // If the scanned character is an operand
            // (number here),extract the number
            // Push it to the stack.
            else if (Character.isDigit(c)) {
                int n = 0;
 
                // Extract the characters and store it in num
                while (Character.isDigit(c)) {
                    n = n * 10 + (int)(c - '0');
                    i++;
                    c = exp.charAt(i);
                }
                i--;
 
                // Push the number in stack
                stack.push(n);
            }
 
            // If the scanned character is an operator, pop
            // two elements from stack apply the operator
            else {
                int val1 = stack.pop();
                int val2 = stack.pop();
 
                switch (c) {
                case '+':
                    stack.push(val2 + val1);
                    break;
                case '-':
                    stack.push(val2 - val1);
                    break;
                case '/':
                    stack.push(val2 / val1);
                    break;
                case '*':
                    stack.push(val2 * val1);
                    break;
                }
            }
        }
        return stack.pop();
    }
 
    // Driver program to test above functions
    public static void main(String[] args)
    {
        String exp = "100 200 + 2 / 5 * 7 +";
       
        // Function call
        System.out.println(evaluatePostfix(exp));
    }
}
 
// This code is contributed by Arnab Kundu

Python3

# Python program to evaluate value of a postfix
# expression with integers containing multiple digits
 
 
class evalpostfix:
    def __init__(self):
        self.stack = []
        self.top = -1
 
    def pop(self):
        if self.top == -1:
            return
        else:
            self.top -= 1
            return self.stack.pop()
 
    def push(self, i):
        self.top += 1
        self.stack.append(i)
 
    def centralfunc(self, ab):
        for i in ab:
 
            # If the component of the list is an integer
            try:
                self.push(int(i))
             
            # If the component of the list is not an integer,
            # it must be an operator. Using ValueError, we can
            # evaluate components of the list other than type int
            except ValueError:
                val1 = self.pop()
                val2 = self.pop()
                if i == '/':
                    self.push(val2 / val1)
                else:
                     
                    # Switch statement to perform operation
                    switcher = {'+': val2 + val1, '-': val2 -
                                val1, '*': val2 * val1, '^': val2**val1}
                    self.push(switcher.get(i))
        return int(self.pop())
 
 
 
# Driver code
if __name__ == '__main__':
    str = '100 200 + 2 / 5 * 7 +'
     
    # Splitting the given string to obtain
    # integers and operators into a list
    strconv = str.split(' ')
    obj = evalpostfix()
    print(obj.centralfunc(strconv))
 
# This code is contributed by Amarnath Reddy

C#

// C# program to evaluate value of a postfix
// expression having multiple digit operands
using System;
using System.Collections.Generic;
 
class GFG {
     
    // Method to evaluate value of
    // a postfix expression
    public static int evaluatePostfix(string exp)
    {
        // Create a stack
        Stack<int> stack = new Stack<int>();
 
        // Scan all characters one by one
        for (int i = 0; i < exp.Length; i++) {
            char c = exp[i];
 
            if (c == ' ') {
                continue;
            }
 
            // If the scanned character is an
            // operand (number here),extract
            // the number. Push it to the stack.
            else if (char.IsDigit(c)) {
                int n = 0;
 
                // Extract the characters and
                // store it in num
                while (char.IsDigit(c)) {
                    n = n * 10 + (int)(c - '0');
                    i++;
                    c = exp[i];
                }
                i--;
 
                // push the number in stack
                stack.Push(n);
            }
 
            // If the scanned character is
            // an operator, pop two elements
            // from stack apply the operator
            else {
                int val1 = stack.Pop();
                int val2 = stack.Pop();
 
                switch (c) {
                case '+':
                    stack.Push(val2 + val1);
                    break;
 
                case '-':
                    stack.Push(val2 - val1);
                    break;
 
                case '/':
                    stack.Push(val2 / val1);
                    break;
 
                case '*':
                    stack.Push(val2 * val1);
                    break;
                }
            }
        }
        return stack.Pop();
    }
 
    // Driver Code
    public static void Main(string[] args)
    {
        string exp = "100 200 + 2 / 5 * 7 +";
       
        // Function call
        Console.WriteLine(evaluatePostfix(exp));
    }
}
 
// This code is contributed by Shrikant13

Javascript

<script>
    // Javascript program to evaluate value of a postfix
    // expression having multiple digit operands
     
    // Method to evaluate value of
    // a postfix expression
    function evaluatePostfix(exp)
    {
        // create a stack
        let stack = [];
 
        // Scan all characters one by one
        for (let i = 0; i < exp.length; i++)
        {
            let c = exp[i];
 
            if (c == ' ')
            {
                continue;
            }
 
            // If the scanned character is an 
            // operand (number here),extract
            // the number. Push it to the stack.
            else if (c >= '0' && c <= '9')
            {
                let n = 0;
 
                // extract the characters and
                // store it in num
                while (c >= '0' && c <= '9')
                {
                    n = n * 10 + (c - '0');
                    i++;
                    c = exp[i];
                }
                i--;
 
                // push the number in stack
                stack.push(n);
            }
 
            // If the scanned character is
            // an operator, pop two elements
            // from stack apply the operator
            else
            {
                let val1 = stack.pop();
                let val2 = stack.pop();
 
                switch (c)
                {
                    case '+':
                    stack.push(val2 + val1);
                    break;
 
                    case '-':
                    stack.push(val2 - val1);
                    break;
 
                    case '/':
                    stack.push(parseInt(val2 / val1, 10));
                    break;
 
                    case '*':
                    stack.push(val2 * val1);
                    break;
                }
            }
        }
        return stack.pop();
    }
     
    let exp = "100 200 + 2 / 5 * 7 +";
    document.write(evaluatePostfix(exp));
 
// This code is contributed by decode2207.
</script>

Output

Time Complexity: O(N)
Auxiliary Space: O(N)

Suggest improvement

Arithmetic Expression Evaluation

How to Reverse a Stack using Recursion

Share your thoughts in the comments

Stack implementation in different language

Some questions related to Stack implementation

Easy problems on Stack

Intermediate problems on Stack

Hard problems on Stack

Stack implementation in different language

Some questions related to Stack implementation

Easy problems on Stack

Intermediate problems on Stack

Hard problems on Stack

Evaluation of Postfix Expression

Evaluation of Postfix Expression using Stack:

C

C++

Java

Python3

C#

Javascript

There are the following limitations of the above implementation.

Postfix evaluation for multi-digit numbers:

C

C++14

Java

Python3

C#

Javascript

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?