Program to check idempotent matrix

Last Updated : 19 Aug, 2022

Given a N * N matrix and the task is to check matrix is idempotent matrix or not.

Idempotent matrix: A matrix is said to be idempotent matrix if matrix multiplied by itself return the same matrix. The matrix M is said to be idempotent matrix if and only if M * M = M. In idempotent matrix M is a square matrix.

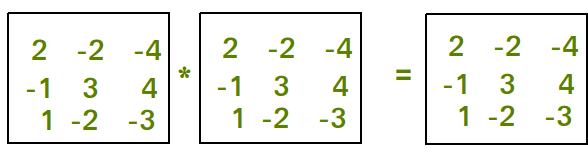
idempotent matrix

Examples:

Input : mat[][] = {{3, -6},
                   {1, -2}};
Output : Idempotent Matrix

Input : mat[N][N] = {{2, -2, -4},
                     {-1, 3, 4},
                     {1, -2, -3}}
Output : Idempotent Matrix.

Implementation:

C++

// Program to check given matrix 
// is idempotent matrix or not.
#include<bits/stdc++.h>
#define N 3
using namespace std;
 
// Function for matrix multiplication.
void multiply(int mat[][N], int res[][N])
{
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        {
            res[i][j] = 0;
            for (int k = 0; k < N; k++)
                res[i][j] += mat[i][k] * mat[k][j];
        }
    }
}
 
// Function to check idempotent
// property of matrix.
bool checkIdempotent(int mat[][N])
{   
    // Calculate multiplication of matrix
    // with itself and store it into res.
    int res[N][N];
    multiply(mat, res);
 
    for (int i = 0; i < N; i++)    
        for (int j = 0; j < N; j++)        
            if (mat[i][j] != res[i][j])
                return false;
    return true;
}
 
// Driver function.
int main()
{
    int mat[N][N] = {{2, -2, -4},
                    {-1, 3, 4},
                    {1, -2, -3}};
     
    // checkIdempotent function call.
    if (checkIdempotent(mat))
        cout << "Idempotent Matrix";
    else
        cout << "Not Idempotent Matrix.";
    return 0;
}

Java

// Java program to check given matrix 
// is idempotent matrix or not.
import java.io.*;
 
class GFG 
{
    static int N = 3;
     
    // Function for matrix multiplication.
    static void multiply(int mat[][], int res[][])
    {
        for (int i = 0; i < N; i++)
        {
            for (int j = 0; j < N; j++)
            {
                res[i][j] = 0;
                for (int k = 0; k < N; k++)
                    res[i][j] += mat[i][k] * mat[k][j];
            }
        }
    }
     
    // Function to check idempotent
    // property of matrix.
    static boolean checkIdempotent(int mat[][])
    { 
        // Calculate multiplication of matrix
        // with itself and store it into res.
        int res[][] = new int[N][N];
        multiply(mat, res);
     
        for (int i = 0; i < N; i++)
        { 
            for (int j = 0; j < N; j++)
            {
                if (mat[i][j] != res[i][j])
                    return false;
            }
        }
        return true;
    }
 
    // Driver code.
    public static void main (String[] args) 
    {
        int mat[][] = {{2, -2, -4},
                       {-1, 3, 4},
                       {1, -2, -3}};
     
        // checkIdempotent function call.
        if (checkIdempotent(mat))
            System.out.println( "Idempotent Matrix");
        else
            System.out.println("Not Idempotent Matrix.");
         
    }
}
 
// This code is contributed by vt_m.

Python 3

# Python Program to check given matrix 
# is idempotent matrix or not.
import math
 
# Function for matrix multiplication.
def multiply(mat, res):
 
    N= len(mat)
    for i in range(0,N):
     
        for j in range(0,N):
         
            res[i][j] = 0
            for k in range(0,N):
                res[i][j] += mat[i][k] * mat[k][j]
 
# Function to check idempotent
# property of matrix.
def checkIdempotent(mat):
 
    N= len(mat)
    # Calculate multiplication of matrix
    # with itself and store it into res.
    res =[[0]*N for i in range(0,N)]
    multiply(mat, res)
 
    for i in range(0,N):
        for j in range(0,N):     
            if (mat[i][j] != res[i][j]):
                return False
    return True
 
# driver Function
mat = [ [2, -2, -4],
        [-1, 3, 4],
        [1, -2, -3] ]
     
# checkIdempotent function call.
if (checkIdempotent(mat)):
    print("Idempotent Matrix")
else:
    print("Not Idempotent Matrix.")
 
# This code is contributed by Gitanjali.

C#

// C# program to check given matrix 
// is idempotent matrix or not.
using System;
 
class GFG 
{
    static int N = 3;
     
    // Function for matrix multiplication.
    static void multiply(int [,]mat, int [,]res)
    {
        for (int i = 0; i < N; i++)
        {
            for (int j = 0; j < N; j++)
            {
                res[i,j] = 0;
                for (int k = 0; k < N; k++)
                    res[i,j] += mat[i,k] * mat[k,j];
            }
        }
    }
     
    // Function to check idempotent
    // property of matrix.
    static bool checkIdempotent(int [,]mat)
    { 
        // Calculate multiplication of matrix
        // with itself and store it into res.
        int [,]res = new int[N,N];
        multiply(mat, res);
     
        for (int i = 0; i < N; i++)
        { 
            for (int j = 0; j < N; j++)
            {
                if (mat[i,j] != res[i,j])
                    return false;
            }
        }
        return true;
    }
 
    // Driver code
    public static void Main () 
    {
        int [,]mat = {{2, -2, 4},
                    {-1, 3, 4},
                    {1, -2, -3}};
     
        // checkIdempotent function call.
        if (checkIdempotent(mat))
            Console.WriteLine( "Idempotent Matrix");
        else
            Console.WriteLine("Not Idempotent Matrix.");
         
    }
}
 
// This code is contributed by vt_m.

Javascript

<script>
  
// Javascript program to check given matrix 
// is idempotent matrix or not.
var N = 3;
 
// Function for matrix multiplication.
function multiply(mat, res)
{
    for (var i = 0; i < N; i++)
    {
        for (var j = 0; j < N; j++)
        {
            res[i][j] = 0;
            for (var k = 0; k < N; k++)
                res[i][j] += mat[i][k] * mat[k][j];
        }
    }
    return res;
}
 
// Function to check idempotent
// property of matrix.
function checkIdempotent(mat)
{ 
 
    // Calculate multiplication of matrix
    // with itself and store it into res.
    var res = Array.from(Array(N), ()=>Array(N).fill(0));
    res = multiply(mat, res);
 
    for (var i = 0; i < N; i++)
    { 
        for (var j = 0; j < N; j++)
        {
            if (mat[i][j] != res[i][j])
                return false;
        }
    }
    return true;
}
 
// Driver code
var mat = [[2, -2, -4],
            [-1, 3, 4],
            [1, -2, -3]];
             
// checkIdempotent function call.
if (checkIdempotent(mat))
    document.write( "Idempotent Matrix");
else
    document.write("Not Idempotent Matrix.");
 
// This code is contributed by noob2000.
</script>

Output

Idempotent Matrix

Time Complexity: O(n³)
Auxiliary Space: O(n²), since n²extra space has been taken.

Suggest improvement

Sum of middle row and column in Matrix

Program to check diagonal matrix and scalar matrix

Share your thoughts in the comments

Basic Operations on Matrix

Easy problems on Matrix

Intermediate problems on Matrix

Hard problems on Matrix