Open In App

Write a function to get the intersection point of two Linked Lists

Last Updated : 16 Apr, 2024
Improve
Improve
Like Article
Like
Save
Share
Report

There are two singly linked lists in a system. By some programming error, the end node of one of the linked lists got linked to the second list, forming an inverted Y-shaped list. Write a program to get the point where two linked lists merge. 

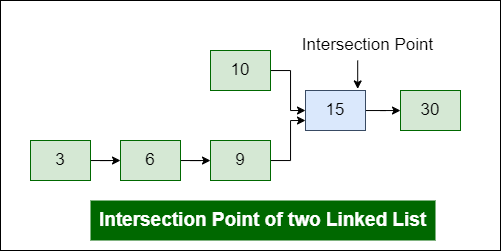
Intersection Point of Two Linked Lists


The above diagram shows an example with two linked lists having 15 as intersection points.

Finding the intersection point using two Nested Loops:

Use 2 nested for loops. The outer loop will be for each node of the 1st list and the inner loop will be for the 2nd list. In the inner loop, check if any of the nodes of the 2nd list is the same as the current node of the first linked list. The time complexity of this method will be O(M * N) where m and n are the numbers of nodes in two lists.

Below is the code for the above approach:

C++ 
// C++ program to get intersection point of two linked list
#include <bits/stdc++.h>
using namespace std;

/* Link list node */
class Node {
public:
    int data;
    Node* next;
      Node(int x) {
        data = x;
          next = NULL;
    }
};

/* function to get the intersection point of two linked
lists head1 and head2 */
Node* getIntesectionNode(Node* head1, Node* head2)
{
    while (head2) {
        Node* temp = head1;
        while (temp) {
            // if both Nodes are same
            if (temp == head2)
                return head2;
            temp = temp->next;
        }
        head2 = head2->next;
    }
    // intersection is not present between the lists
    return NULL;
}

// Driver Code
int main()
{
    /*
        Create two linked lists

        1st 3->6->9->15->30
        2nd 10->15->30

        15 is the intersection point
    */

    Node* newNode;

    // Addition of new nodes
    Node* head1 = new Node(10);
    Node* head2 = new Node(3);
  
    head2->next = new Node(6);
    head2->next->next = new Node(9);

    newNode = new Node(15);
    head1->next = newNode;
    head2->next->next->next = newNode;

    newNode = new Node(30);
    head1->next->next = newNode;

    head1->next->next->next = NULL;

    Node* intersectionPoint
        = getIntesectionNode(head1, head2);

    if (!intersectionPoint)
        cout << " No Intersection Point \n";
    else
        cout << "Intersection Point: "
             << intersectionPoint->data << endl;
}

// This code is contributed by Tapesh(tapeshdua420)
C 
// C program to get intersection point of two linked list
#include <stdio.h>
#include <stdlib.h>

/* Link list node */
typedef struct Node {
    int data;
    struct Node* next;
} Node;

/* function to get the intersection point of two linked
lists head1 and head2 */
Node* getIntesectionNode(Node* head1, Node* head2)
{
    while (head2) {
        Node* temp = head1;
        while (temp) {
            // if both Nodes are same
            if (temp == head2)
                return head2;
            temp = temp->next;
        }
        head2 = head2->next;
    }
    // intersection is not present between the lists
    return NULL;
}

// Driver Code
int main()
{
    /*
        Create two linked lists

        1st 3->6->9->15->30
        2nd 10->15->30

        15 is the intersection point
    */

    Node* newNode;

    // Addition of new nodes
    Node* head1 = (Node*)malloc(sizeof(Node));
    head1->data = 10;

    Node* head2 = (Node*)malloc(sizeof(Node));
    head2->data = 3;

    newNode = (Node*)malloc(sizeof(Node));
    newNode->data = 6;
    head2->next = newNode;

    newNode = (Node*)malloc(sizeof(Node));
    newNode->data = 9;
    head2->next->next = newNode;

    newNode = (Node*)malloc(sizeof(Node));
    newNode->data = 15;
    head1->next = newNode;
    head2->next->next->next = newNode;

    newNode = (Node*)malloc(sizeof(Node));
    newNode->data = 30;
    head1->next->next = newNode;

    head1->next->next->next = NULL;

    Node* intersectionPoint
        = getIntesectionNode(head1, head2);

    if (!intersectionPoint)
        printf(" No Intersection Point \n");
    else
        printf("Intersection Point: %d\n",
               intersectionPoint->data);
}

// This code is contributed by Aditya Kumar (adityakumar129)
Java 
// Java Program to get intersection point of two linked
// lists.
import java.util.*;
import java.io.*;


class GFG {

    static class Node {
        int data;
        Node next;
        Node(int d)
        {
            data = d;
            next = null;
        }
    }

    /* function to get the intersection point of two linked
    lists head1 and head2 */
    public Node getIntersectionNode(Node head1, Node head2)
    {
        while (head2 != null) {
            Node temp = head1;
            while (temp != null) {
                // if both Nodes are same
                if (temp == head2) {
                    return head2;
                }
                temp = temp.next;
            }
            head2 = head2.next;
        }
        // If intersection is not present between the lists,
        // return NULL.
        return null;
    }

    public static void main(String[] args)
    {
        GFG list = new GFG();

        Node head1, head2;

        /*
                Create two linked lists

                1st 3->6->9->15->30
                2nd 10->15->30

                15 is the intersection point
        */

        head1 = new Node(10);
        head2 = new Node(3);

        Node newNode = new Node(6);
        head2.next = newNode;

        newNode = new Node(9);
        head2.next.next = newNode;

        newNode = new Node(15);
        head1.next = newNode;
        head2.next.next.next = newNode;

        newNode = new Node(30);
        head1.next.next = newNode;

        head1.next.next.next = null;

        Node intersectionPoint
            = list.getIntersectionNode(head1, head2);

        if (intersectionPoint == null) {
            System.out.print(" No Intersection Point \n");
        }
        else {
            System.out.print("Intersection Point: "
                             + intersectionPoint.data);
        }
    }
}

// This code is contributed by lokesh (lokeshmvs21).
Python3 
# Python program to get intersection point of two linked list

# Link list node
class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

# function to get the intersection point of two linked lists head1 and head
def getIntersectionNode(head1, head2):
    while head2:
        temp = head1
        while temp:
            # if both Nodes are same
            if temp == head2:
                return head2
            temp = temp.next
        head2 = head2.next
    # intersection is not present between the lists
    return None


# Driver Code
if __name__ == '__main__':
    '''
    Create two linked lists

    1st 3->6->9->15->30
    2nd 10->15->30

    15 is the intersection point 
    '''

    newNode = Node(10)
    head1 = newNode
    newNode = Node(3)
    head2 = newNode
    newNode = Node(6)
    head2.next = newNode
    newNode = Node(9)
    head2.next.next = newNode
    newNode = Node(15)
    head1.next = newNode
    head2.next.next.next = newNode
    newNode = Node(30)
    head1.next.next = newNode

    intersectionPoint = getIntersectionNode(head1, head2)

    if not intersectionPoint:
        print(" No Intersection Point ")
    else:
        print("Intersection Point:", intersectionPoint.data)

# This code is contributed by Tapesh(tapeshdua420)
C# 
// C# program to get intersection point of two linked
// lists.
using System;

class GFG {

  public class Node {
    public int data;
    public Node next;
    public Node(int d)
    {
      data = d;
      next = null;
    }
  }
  
  /* function to get the intersection point of two linked
     * lists head1 and head2 */
  public Node getIntersectionNode(Node head1, Node head2)
  {
    while (head2 != null) {
      Node temp = head1;
      while (temp != null)
      {
        
        // if both Nodes are same
        if (temp == head2) {
          return head2;
        }
        temp = temp.next;
      }
      head2 = head2.next;
    }
    
    // If intersection is not present between the lists,
    // return NULL.
    return null;
  }
  public static void Main(string[] args)
  {
    GFG list = new GFG();
    Node head1, head2;

    /*
                Create two linked lists

                1st 3->6->9->15->30
                2nd 10->15->30

                15 is the intersection point
        */

    head1 = new Node(10);
    head2 = new Node(3);

    Node newNode = new Node(6);
    head2.next = newNode;

    newNode = new Node(9);
    head2.next.next = newNode;

    newNode = new Node(15);
    head1.next = newNode;
    head2.next.next.next = newNode;

    newNode = new Node(30);
    head1.next.next = newNode;

    head1.next.next.next = null;

    Node intersectionPoint
      = list.getIntersectionNode(head1, head2);

    if (intersectionPoint == null) {
      Console.Write(" No Intersection Point \n");
    }
    else {
      Console.Write("Intersection Point: "
                    + intersectionPoint.data);
    }
  }
}

// This code is contributed by Tapesh(tapeshdua420).
Javascript 
// JS code for finding intersection point
class Node {
    constructor(d) {
        this.data = d;
        this.next = null;
    }
}

function getIntesectionNode(head1, head2) {
    while (head2) {
        let temp = head1;
        while (temp) {
            if (temp == head2) {
                return head2;
            }
            temp = temp.next;
        }
        head2 = head2.next;
    }
    return null;
}

let newNode = new Node();

let head1 = new Node();
head1.data = 10;


let head2 = new Node();
head2.data = 3;

newNode = new Node();
newNode.data = 6;
head2.next = newNode;

newNode = new Node();
newNode.data = 9;
head2.next.next = newNode;

newNode = new Node();
newNode.data = 15;
head1.next = newNode;
head2.next.next.next = newNode;

newNode = new Node();
newNode.data = 30;
head1.next.next = newNode;

head1.next.next.next = null;

let intersectionPoint = getIntesectionNode(head1, head2);

if (!intersectionPoint)
    console.log(" No Intersection Point");
else
    console.log("Intersection Point: ", intersectionPoint.data);


// This code is contributed by adityamaharshi21

Output
Intersection Point: 15

Time Complexity: O(m*n), where m and n are number of nodes in two linked list.
Auxiliary Space: O(1), Constant Space is used.

Finding the intersection point using Hashing:

Basically, we need to find a common node of two linked lists. So, we store all the nodes of the first list in a hash set and then iterate over second list checking if the node is present in the set. If we find a node which is present in the hash set, we return the node.

Step-by-step approach:

  • Create an empty hash set.
  • Traverse the first linked list and insert all nodes’ addresses in the hash set.
  • Traverse the second list. For every node check if it is present in the hash set. If we find a node in the hash set, return the node.

Below is the implementation of the above approach:

C++ 
// C++ program to get intersection point of two linked list
#include <iostream>
#include <unordered_set>
using namespace std;
class Node
{
public:
    int data;
    Node* next;
     Node(int d)
    {
      data = d;
      next = NULL;
    }
};

// function to find the intersection point of two lists
void MegeNode(Node* n1, Node* n2)
{
    unordered_set<Node*> hs;
    while (n1 != NULL) {
        hs.insert(n1);
        n1 = n1->next;
    }
    while (n2) {
        if (hs.find(n2) != hs.end()) {
            cout << n2->data << endl;
            break;
        }
        n2 = n2->next;
    }
}

// function to print the list
void Print(Node* n)
{
      Node* curr = n;
      while(curr != NULL){
      cout << curr->data << " ";
      curr = curr->next;
    }
      cout << endl;
}
  
int main() 
{
     // list 1
     Node* n1 = new Node(1);
     n1->next = new Node(2);
     n1->next->next = new Node(3);
     n1->next->next->next = new Node(4);
     n1->next->next->next->next = new Node(5);
     n1->next->next->next->next->next = new Node(6);
     n1->next->next->next->next->next->next = new Node(7);
     // list 2
     Node* n2 = new Node(10);
     n2->next = new Node(9);
     n2->next->next = new Node(8);
     n2->next->next->next = n1->next->next->next;
     Print(n1);
     Print(n2);
          
       MegeNode(n1,n2);
      
       return 0;
}

 // This code is contributed by Upendra
Java 
// Java program to get intersection point of two linked list
import java.util.*;
class Node {
    int data;
    Node next;
    Node(int d)
    {
        data = d;
        next = null;
    }
}
class LinkedListIntersect {
    public static void main(String[] args)
    {
        // list 1
        Node n1 = new Node(1);
        n1.next = new Node(2);
        n1.next.next = new Node(3);
        n1.next.next.next = new Node(4);
        n1.next.next.next.next = new Node(5);
        n1.next.next.next.next.next = new Node(6);
        n1.next.next.next.next.next.next = new Node(7);
        // list 2
        Node n2 = new Node(10);
        n2.next = new Node(9);
        n2.next.next = new Node(8);
        n2.next.next.next = n1.next.next.next;
        Print(n1);
        Print(n2);
        System.out.println(MegeNode(n1, n2).data);
    }

    // function to print the list
    public static void Print(Node n)
    {
        Node cur = n;
        while (cur != null) {
            System.out.print(cur.data + "  ");
            cur = cur.next;
        }
        System.out.println();
    }

    // function to find the intersection of two node
    public static Node MegeNode(Node n1, Node n2)
    {
        // define hashset
        HashSet<Node> hs = new HashSet<Node>();
        while (n1 != null) {
            hs.add(n1);
            n1 = n1.next;
        }
        while (n2 != null) {
            if (hs.contains(n2)) {
                return n2;
            }
            n2 = n2.next;
        }
        return null;
    }
}
Python3 
# Python program to get intersection 
# point of two linked list
class Node :
    def __init__(self, d):
        self.data = d;
        self.next = None;

# Function to print the list
def Print(n):
    cur = n;
    while (cur != None) :
        print(cur.data, end=" ");
        cur = cur.next;
    print("");

# Function to find the intersection of two node
def MegeNode(n1, n2):
    
    # Define hashset
    hs = set();

    while (n1 != None):
        hs.add(n1);
        n1 = n1.next;
    while (n2 != None):
        if (n2 in hs):
            return n2;
        n2 = n2.next;
    
    return None;


# Driver code

# list 1
n1 = Node(1);
n1.next = Node(2);
n1.next.next = Node(3);
n1.next.next.next = Node(4);
n1.next.next.next.next = Node(5);
n1.next.next.next.next.next = Node(6);
n1.next.next.next.next.next.next = Node(7);

# list 2
n2 = Node(10);
n2.next = Node(9);
n2.next.next = Node(8);
n2.next.next.next = n1.next.next.next;

Print(n1);
Print(n2);

print(MegeNode(n1, n2).data);

# This code is contributed by _saurabh_jaiswal
C# 
// C# program to get intersection point of two linked list
using System;
using System.Collections.Generic; 

public class Node 
{
    public int data;
    public Node next;
    public Node(int d)
    {
        data = d;
        next = null;
    }
}
public class LinkedListIntersect
{
    public static void Main(String[] args)
    {
        // list 1
        Node n1 = new Node(1);
        n1.next = new Node(2);
        n1.next.next = new Node(3);
        n1.next.next.next = new Node(4);
        n1.next.next.next.next = new Node(5);
        n1.next.next.next.next.next = new Node(6);
        n1.next.next.next.next.next.next = new Node(7);
        // list 2
        Node n2 = new Node(10);
        n2.next = new Node(9);
        n2.next.next = new Node(8);
        n2.next.next.next = n1.next.next.next;
        Print(n1);
        Print(n2);
        Console.WriteLine(MegeNode(n1, n2).data);
    }

    // function to print the list
    public static void Print(Node n)
    {
        Node cur = n;
        while (cur != null) 
        {
            Console.Write(cur.data + " ");
            cur = cur.next;
        }
        Console.WriteLine();
    }

    // function to find the intersection of two node
    public static Node MegeNode(Node n1, Node n2)
    {
        // define hashset
        HashSet<Node> hs = new HashSet<Node>();
        while (n1 != null) 
        {
            hs.Add(n1);
            n1 = n1.next;
        }
        while (n2 != null)
        {
            if (hs.Contains(n2)) 
            {
                return n2;
            }
            n2 = n2.next;
        }
        return null;
    }
}

// This code is contributed by 29AjayKumar
Javascript 
<script>

// Javascript program to get intersection 
// point of two linked list
class Node 
{
    constructor(d)
    {
        this.data = d;
        this.next = null;
    }
}

// Function to print the list
function Print(n)
{
    let cur = n;
    while (cur != null) 
    {
        document.write(cur.data + "  ");
        cur = cur.next;
    }
    document.write("<br>");
}

// Function to find the intersection of two node
function MegeNode(n1, n2)
{
    
    // Define hashset
    let hs = new Set();
    while (n1 != null)
    {
        hs.add(n1);
        n1 = n1.next;
    }
    while (n2 != null)
    {
        if (hs.has(n2))
        {
            return n2;
        }
        n2 = n2.next;
    }
    return null;
}

// Driver code

// list 1
let n1 = new Node(1);
n1.next = new Node(2);
n1.next.next = new Node(3);
n1.next.next.next = new Node(4);
n1.next.next.next.next = new Node(5);
n1.next.next.next.next.next = new Node(6);
n1.next.next.next.next.next.next = new Node(7);

// list 2
let n2 = new Node(10);
n2.next = new Node(9);
n2.next.next = new Node(8);
n2.next.next.next = n1.next.next.next;

Print(n1);
Print(n2);

document.write(MegeNode(n1, n2).data);

// This code is contributed by rag2127

</script>

Output
1 2 3 4 5 6 7 
10 9 8 4 5 6 7 
4

Time complexity: O(n), where n is the length of the longer list. This is because we need to traverse both of the linked lists in order to find the intersection point.
Auxiliary Space: O(n) , because we are using unordered set.

Find the intersection point using difference in node counts:

In this method, we find the difference (D) between the count of nodes in both the lists. Then, we increment the start pointer of the longer list by D nodes. Now, we have both start pointers at the same distance from the intersection point, so we can keep incrementing both the start pointers until we find the intersection point.

  • Get the count of the nodes in the first list, let the count be c1.
  • Get the count of the nodes in the second list, let the count be c2.
  • Get the difference of counts d = abs(c1 – c2)
  • Now traverse the bigger list from the first node to d nodes so that from here onwards both the lists have an equal no of nodes
  • Then we can traverse both lists in parallel till we come across a common node. (Note that getting a common node is done by comparing the address of the nodes)

Illustration:

Step 1:  Traverse the bigger list from the first node to d nodes so that from here onwards both the lists have an equal no of nodes

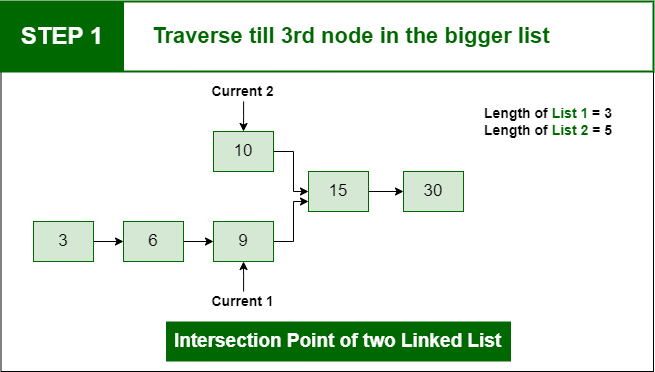
Step 1

Step 2:  Traverse both lists in parallel till we come across a common node

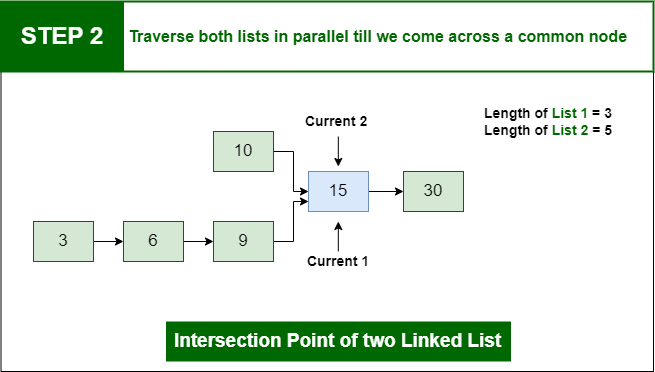
Step 2

Below is the implementation of the above approach :

C++ 
// C++ program to get intersection point of two linked list
#include <bits/stdc++.h>
using namespace std;

/* Link list node */
class Node {
public:
    int data;
    Node* next;
      Node(int x) {
        data = x;
          next = NULL;
    }
};

/* Function to get the counts of node in a linked list */
int getCount(Node* head);

/* function to get the intersection point of two linked 
lists head1 and head2 where head1 has d more nodes than 
head2 */
int _getIntesectionNode(int d, Node* head1, Node* head2);

/* function to get the intersection point of two linked 
lists head1 and head2 */
int getIntesectionNode(Node* head1, Node* head2)
{

    // Count the number of nodes in
    // both the linked list
    int c1 = getCount(head1);
    int c2 = getCount(head2);
    int d;

    // If first is greater
    if (c1 > c2) {
        d = c1 - c2;
        return _getIntesectionNode(d, head1, head2);
    }
    else {
        d = c2 - c1;
        return _getIntesectionNode(d, head2, head1);
    }
}

/* function to get the intersection point of two linked 
lists head1 and head2 where head1 has d more nodes than 
head2 */
int _getIntesectionNode(int d, Node* head1, Node* head2)
{
    // Stand at the starting of the bigger list
    Node* current1 = head1;
    Node* current2 = head2;

    // Move the pointer forward
    for (int i = 0; i < d; i++) {
        if (current1 == NULL) {
            return -1;
        }
        current1 = current1->next;
    }

    // Move both pointers of both list till they
    // intersect with each other
    while (current1 != NULL && current2 != NULL) {
        if (current1 == current2)
            return current1->data;

        // Move both the pointers forward
        current1 = current1->next;
        current2 = current2->next;
    }

    return -1;
}

/* Takes head pointer of the linked list and 
returns the count of nodes in the list */
int getCount(Node* head)
{
    Node* current = head;

    // Counter to store count of nodes
    int count = 0;

    // Iterate till NULL
    while (current != NULL) {

        // Increase the counter
        count++;

        // Move the Node ahead
        current = current->next;
    }

    return count;
}

// Driver Code
int main()
{
    /* 
        Create two linked lists 
    
        1st 3->6->9->15->30 
        2nd 10->15->30 
    
        15 is the intersection point 
    */

    Node* newNode;

    // Addition of new nodes
    Node* head1 = new Node(10);
    Node* head2 = new Node(3);

    newNode = new Node(6);
    head2->next = newNode;

    newNode = new Node(9);
    head2->next->next = newNode;

    newNode = new Node(15);
    head1->next = newNode;
    head2->next->next->next = newNode;

    newNode = new Node(30);
    head1->next->next = newNode;

    head1->next->next->next = NULL;

    cout << "The node of intersection is " << getIntesectionNode(head1, head2);
}

// This code is contributed by rathbhupendra
C 
// C program to get intersection point of two linked list
#include <stdio.h>
#include <stdlib.h>

/* Link list node */
struct Node {
    int data;
    struct Node* next;
};

/* Function to get the counts of node in a linked list */
int getCount(struct Node* head);

/* function to get the intersection point of two linked
   lists head1 and head2 where head1 has d more nodes than
   head2 */
int _getIntesectionNode(int d, struct Node* head1, struct Node* head2);

/* function to get the intersection point of two linked
   lists head1 and head2 */
int getIntesectionNode(struct Node* head1, struct Node* head2)
{
    int c1 = getCount(head1);
    int c2 = getCount(head2);
    int d;

    if (c1 > c2) {
        d = c1 - c2;
        return _getIntesectionNode(d, head1, head2);
    }
    else {
        d = c2 - c1;
        return _getIntesectionNode(d, head2, head1);
    }
}

/* function to get the intersection point of two linked
   lists head1 and head2 where head1 has d more nodes than
   head2 */
int _getIntesectionNode(int d, struct Node* head1, struct Node* head2)
{
    int i;
    struct Node* current1 = head1;
    struct Node* current2 = head2;

    for (i = 0; i < d; i++) {
        if (current1 == NULL) {
            return -1;
        }
        current1 = current1->next;
    }

    while (current1 != NULL && current2 != NULL) {
        if (current1 == current2)
            return current1->data;
        current1 = current1->next;
        current2 = current2->next;
    }

    return -1;
}

/* Takes head pointer of the linked list and
   returns the count of nodes in the list */
int getCount(struct Node* head)
{
    struct Node* current = head;
    int count = 0;

    while (current != NULL) {
        count++;
        current = current->next;
    }

    return count;
}

/* IGNORE THE BELOW LINES OF CODE. THESE LINES
   ARE JUST TO QUICKLY TEST THE ABOVE FUNCTION */
int main()
{
    /*
    Create two linked lists

    1st 3->6->9->15->30
    2nd 10->15->30

    15 is the intersection point
  */

    struct Node* newNode;
    struct Node* head1 = (struct Node*)malloc(sizeof(struct Node));
    head1->data = 10;

    struct Node* head2 = (struct Node*)malloc(sizeof(struct Node));
    head2->data = 3;

    newNode = (struct Node*)malloc(sizeof(struct Node));
    newNode->data = 6;
    head2->next = newNode;

    newNode = (struct Node*)malloc(sizeof(struct Node));
    newNode->data = 9;
    head2->next->next = newNode;

    newNode = (struct Node*)malloc(sizeof(struct Node));
    newNode->data = 15;
    head1->next = newNode;
    head2->next->next->next = newNode;

    newNode = (struct Node*)malloc(sizeof(struct Node));
    newNode->data = 30;
    head1->next->next = newNode;

    head1->next->next->next = NULL;

    printf("\n The node of intersection is %d \n",
           getIntesectionNode(head1, head2));

    getchar();
}
Java 
// Java program to get intersection point of two linked list

class LinkedList {

    static Node head1, head2;

    static class Node {

        int data;
        Node next;

        Node(int d)
        {
            data = d;
            next = null;
        }
    }

    /*function to get the intersection point of two linked
    lists head1 and head2 */
    int getNode()
    {
        int c1 = getCount(head1);
        int c2 = getCount(head2);
        int d;

        if (c1 > c2) {
            d = c1 - c2;
            return _getIntesectionNode(d, head1, head2);
        }
        else {
            d = c2 - c1;
            return _getIntesectionNode(d, head2, head1);
        }
    }

    /* function to get the intersection point of two linked
     lists head1 and head2 where head1 has d more nodes than
     head2 */
    int _getIntesectionNode(int d, Node node1, Node node2)
    {
        int i;
        Node current1 = node1;
        Node current2 = node2;
        for (i = 0; i < d; i++) {
            if (current1 == null) {
                return -1;
            }
            current1 = current1.next;
        }
        while (current1 != null && current2 != null) {
            if (current1.data == current2.data) {
                return current1.data;
            }
            current1 = current1.next;
            current2 = current2.next;
        }

        return -1;
    }

    /*Takes head pointer of the linked list and
    returns the count of nodes in the list */
    int getCount(Node node)
    {
        Node current = node;
        int count = 0;

        while (current != null) {
            count++;
            current = current.next;
        }

        return count;
    }

    public static void main(String[] args)
    {
        LinkedList list = new LinkedList();

        // creating first linked list
        list.head1 = new Node(3);
        list.head1.next = new Node(6);
        list.head1.next.next = new Node(9);
        list.head1.next.next.next = new Node(15);
        list.head1.next.next.next.next = new Node(30);

        // creating second linked list
        list.head2 = new Node(10);
        list.head2.next = new Node(15);
        list.head2.next.next = new Node(30);

        System.out.println("The node of intersection is " + list.getNode());
    }
}

// This code has been contributed by Mayank Jaiswal
Python3 
# defining a node for LinkedList
class Node:
  def __init__(self,data):
    self.data=data
    self.next=None
    


def getIntersectionNode(head1,head2):
  
  #finding the total number of elements in head1 LinkedList
    c1=getCount(head1)
  
  #finding the total number of elements in head2 LinkedList
    c2=getCount(head2)
  
  #Traverse the bigger node by 'd' so that from that node onwards, both LinkedList
  #would be having same number of nodes and we can traverse them together.
    if c1 > c2:
        d=c1-c2
        return _getIntersectionNode(d,head1,head2)
    else:
        d=c2-c1
        return _getIntersectionNode(d,head2,head1) 
  
  
def _getIntersectionNode(d,head1,head2):
    
    
    current1=head1
    current2=head2
    
    
    for i in range(d):
        if current1 is None:
            return -1
        current1=current1.next
    
    while current1 is not None and current2 is not None:
    
    # Instead of values, we need to check if there addresses are same
    # because there can be a case where value is same but that value is
    #not an intersecting point.
        if current1 is current2:
            return current1.data # or current2.data ( the value would be same)
    
        current1=current1.next
        current2=current2.next
  
  # Incase, we are not able to find our intersecting point.
    return -1
  
#Function to get the count of a LinkedList
def getCount(node):
    cur=node
    count=0
    while cur is not None:
        count+=1
        cur=cur.next
    return count
    

if __name__ == '__main__':
  # Creating two LinkedList
  # 1st one: 3->6->9->15->30
  # 2nd one: 10->15->30
  # We can see that 15 would be our intersection point
  
  # Defining the common node
  
  common=Node(15)
  
  #Defining first LinkedList
  
  head1=Node(3)
  head1.next=Node(6)
  head1.next.next=Node(9)
  head1.next.next.next=common
  head1.next.next.next.next=Node(30)
  
  # Defining second LinkedList
  
  head2=Node(10)
  head2.next=common
  head2.next.next=Node(30)
  
  print("The node of intersection is ",getIntersectionNode(head1,head2))
  
  # The code is contributed by Ansh Gupta.
C# 
// C# program to get intersection point of two linked list
using System;
class LinkedList {

    Node head1, head2;

    public class Node {

        public int data;
        public Node next;

        public Node(int d)
        {
            data = d;
            next = null;
        }
    }

    /*function to get the intersection point of two linked 
    lists head1 and head2 */
    int getNode()
    {
        int c1 = getCount(head1);
        int c2 = getCount(head2);
        int d;

        if (c1 > c2) {
            d = c1 - c2;
            return _getIntesectionNode(d, head1, head2);
        }
        else {
            d = c2 - c1;
            return _getIntesectionNode(d, head2, head1);
        }
    }

    /* function to get the intersection point of two linked 
    lists head1 and head2 where head1 has d more nodes than 
    head2 */
    int _getIntesectionNode(int d, Node node1, Node node2)
    {
        int i;
        Node current1 = node1;
        Node current2 = node2;
        for (i = 0; i < d; i++) {
            if (current1 == null) {
                return -1;
            }
            current1 = current1.next;
        }
        while (current1 != null && current2 != null) {
            if (current1.data == current2.data) {
                return current1.data;
            }
            current1 = current1.next;
            current2 = current2.next;
        }

        return -1;
    }

    /*Takes head pointer of the linked list and 
    returns the count of nodes in the list */
    int getCount(Node node)
    {
        Node current = node;
        int count = 0;

        while (current != null) {
            count++;
            current = current.next;
        }

        return count;
    }

    public static void Main(String[] args)
    {
        LinkedList list = new LinkedList();

        // creating first linked list
        list.head1 = new Node(3);
        list.head1.next = new Node(6);
        list.head1.next.next = new Node(9);
        list.head1.next.next.next = new Node(15);
        list.head1.next.next.next.next = new Node(30);

        // creating second linked list
        list.head2 = new Node(10);
        list.head2.next = new Node(15);
        list.head2.next.next = new Node(30);

        Console.WriteLine("The node of intersection is " + list.getNode());
    }
}

// This code is contributed by Arnab Kundu
Javascript 
<script>


class Node
{
    constructor(item)
    {
        this.data=item;
        this.next=null;
    }
}

let head1,head2;
function getNode()
{
    let c1 = getCount(head1);
        let c2 = getCount(head2);
        
        let d;
  
        if (c1 > c2) {
            d = c1 - c2;
            return _getIntesectionNode(d, head1, head2);
        }
        else {
            d = c2 - c1;
            return _getIntesectionNode(d, head2, head1);
        }
}

function _getIntesectionNode(d,node1,node2)
{
    let i;
        let current1 = node1;
        let current2 = node2;
        for (i = 0; i < d; i++) {
            if (current1 == null) {
                return -1;
            }
            current1 = current1.next;
        }
        while (current1 != null && current2 != null) {
            if (current1.data == current2.data) {
                return current1.data;
            }
            current1 = current1.next;
            current2 = current2.next;
        }
  
        return -1;
}

function getCount(node)
{
    let current = node;
        let count = 0;
  
        while (current != null) {
            count++;
            current = current.next;
        }
  
        return count;
}

head1 = new Node(3);
head1.next = new Node(6);
head1.next.next = new Node(9);
head1.next.next.next = new Node(15);
head1.next.next.next.next = new Node(30);

// creating second linked list
head2 = new Node(10);
head2.next = new Node(15);
head2.next.next = new Node(30);

document.write("The node of intersection is " + getNode());



// This code is contributed by avanitrachhadiya2155

</script>

Output
The node of intersection is 15

Time Complexity: O(m+n) 
Auxiliary Space: O(1)

Find the intersection point using Two Pointer Technique:

This algorithm works by traversing the two linked lists simultaneously, using two pointers. When one pointer reaches the end of its list, it is reassigned to the head of the other list. This process continues until the two pointers meet, which indicates that they have reached the intersection point.

Steps to solve the problem:

  • Initialize two pointers ptr1 and ptr2  at head1 and  head2.
  • Traverse through the lists, one node at a time.
    • When ptr1 reaches the end of a list, then redirect it to head2.
    • Similarly, when ptr2 reaches the end of a list, redirect it to the head1.
    • Once both of them go through reassigning, they will be equidistant from the collision point
    • If at any node ptr1 meets ptr2, then it is the intersection node.
  • After the second iteration if there is no intersection node it returns NULL.

Below is the implementation of the above approach:

C++ 
// CPP program to print intersection of lists
#include <bits/stdc++.h>
using namespace std;

/* Link list node */
class Node {
public:
    int data;
    Node* next;
      Node(int x) {
        data = x;
         next = NULL;
    }
};

// A utility function to return  intersection node
Node* intersectPoint(Node* head1, Node* head2)
{
    // Maintaining two pointers ptr1 and ptr2
    // at the head of A and B,
    Node* ptr1 = head1;
    Node* ptr2 = head2;

    // If any one of head is NULL i.e
    // no Intersection Point
    if (ptr1 == NULL || ptr2 == NULL)
        return NULL;

    // Traverse through the lists until they
    // reach Intersection node
    while (ptr1 != ptr2) {

        ptr1 = ptr1->next;
        ptr2 = ptr2->next;

        // If at any node ptr1 meets ptr2, then it is
        // intersection node.Return intersection node.

        if (ptr1 == ptr2)
            return ptr1;
        /* Once both of them go through reassigning,
        they will be equidistant from the collision point.*/

        // When ptr1 reaches the end of a list, then
        // reassign it to the head2.
        if (ptr1 == NULL)
            ptr1 = head2;
        // When ptr2 reaches the end of a list, then
        // redirect it to the head1.
        if (ptr2 == NULL)
            ptr2 = head1;
    }
    return ptr1;
}

// Driver code
int main()
{
    /*
    Create two linked lists

    1st Linked list is 3->6->9->15->30
    2nd Linked list is 10->15->30

    15 30 are elements in the intersection list
    */

    Node* newNode;
    Node* head1 = new Node(10);
    Node* head2 = new Node(3);
    newNode = new Node(6);
    head2->next = newNode;
    newNode = new Node(9);
    head2->next->next = newNode;
    newNode = new Node(15);
    head1->next = newNode;
    head2->next->next->next = newNode;
    newNode = new Node(30);
    head1->next->next = newNode;
    head1->next->next->next = NULL;
    Node* intersect_node = NULL;

    // Find the intersection node of two linked lists
    intersect_node = intersectPoint(head1, head2);
    if(intersect_node == NULL)
      cout << "No intersection Point";
      else 
      cout << "Intersection Point = " << intersect_node->data << "\n";
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)
C 
// c program to print intersection of lists
#include <stdio.h>
#include <stdlib.h>

/* Link list node */
typedef struct Node {
    int data;
    struct Node* next;
}Node;

// A utility function to return  intersection node
Node* intersectPoint(Node* head1, Node* head2)
{
    // Maintaining two pointers ptr1 and ptr2
    // at the head of A and B,
    Node* ptr1 = head1;
    Node* ptr2 = head2;

    // If any one of head is NULL i.e
    // no Intersection Point
    if (ptr1 == NULL || ptr2 == NULL)
        return NULL;

    // Traverse through the lists until they
    // reach Intersection node
    while (ptr1 != ptr2) {

        ptr1 = ptr1->next;
        ptr2 = ptr2->next;

        // If at any node ptr1 meets ptr2, then it is
        // intersection node.Return intersection node.

        if (ptr1 == ptr2)
            return ptr1;
        /* Once both of them go through reassigning,
        they will be equidistant from the collision point.*/

        // When ptr1 reaches the end of a list, then
        // reassign it to the head2.
        if (ptr1 == NULL)
            ptr1 = head2;
        // When ptr2 reaches the end of a list, then
        // redirect it to the head1.
        if (ptr2 == NULL)
            ptr2 = head1;
    }
    return ptr1;
}

// Driver code
int main()
{
    /*
    Create two linked lists

    1st Linked list is 3->6->9->15->30
    2nd Linked list is 10->15->30

    15 30 are elements in the intersection list
    */
    Node* newNode;
    Node* head1 = (Node*)malloc(sizeof(Node));
    head1->data = 10;
    Node* head2 = (Node*)malloc(sizeof(Node));
    head2->data = 3;
    newNode = (Node*)malloc(sizeof(Node));
    newNode->data = 6;
    head2->next = newNode;
    newNode = (Node*)malloc(sizeof(Node));
    newNode->data = 9;
    head2->next->next = newNode;
    newNode = (Node*)malloc(sizeof(Node));
    newNode->data = 15;
    head1->next = newNode;
    head2->next->next->next = newNode;
    newNode = (Node*)malloc(sizeof(Node));
    newNode->data = 30;
    head1->next->next = newNode;
    head1->next->next->next = NULL;
    Node* intersect_node = NULL;

    // Find the intersection node of two linked lists
    intersect_node = intersectPoint(head1, head2);
    if(intersect_node == NULL)
      printf("No Intersection Point");
      else
      printf("Intersection Point = %d", intersect_node->data);
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)
Java 
// JAVA program to print intersection of lists

import java.util.*;

class GFG{

/* Link list node */
static class Node {
    int data;
    Node next;
      Node(int x) {
        data = x;
          next = null;
    }
};

// A utility function to return  intersection node
static Node intersectPoint(Node head1, Node head2)
{
    // Maintaining two pointers ptr1 and ptr2
    // at the head of A and B,
    Node ptr1 = head1;
    Node ptr2 = head2;

    // If any one of head is null i.e
    // no Intersection Point
    if (ptr1 == null || ptr2 == null) {

        return null;
    }

    // Traverse through the lists until they
    // reach Intersection node
    while (ptr1 != ptr2) {

        ptr1 = ptr1.next;
        ptr2 = ptr2.next;

        // If at any node ptr1 meets ptr2, then it is
        // intersection node.Return intersection node.

        if (ptr1 == ptr2) {

            return ptr1;
        }
        /* Once both of them go through reassigning,
        they will be equidistant from the collision point.*/

        // When ptr1 reaches the end of a list, then
        // reassign it to the head2.
        if (ptr1 == null) {

            ptr1 = head2;
        }
        // When ptr2 reaches the end of a list, then
        // redirect it to the head1.
        if (ptr2 == null) {

            ptr2 = head1;
        }
    }

    return ptr1;
}
  
// Driver code
public static void main(String[] args)
{
    /*
    Create two linked lists

    1st Linked list is 3.6.9.15.30
    2nd Linked list is 10.15.30

    15 30 are elements in the intersection list
    */

    Node newNode;
    Node head1 = new Node(10);
    Node head2 = new Node(3);
    newNode = new Node(6);
    head2.next = newNode;
    newNode = new Node(9);
    head2.next.next = newNode;
    newNode = new Node(15);
    head1.next = newNode;
    head2.next.next.next = newNode;
    newNode = new Node(30);
    head1.next.next = newNode;
    head1.next.next.next = null;
    Node intersect_node = null;

    // Find the intersection node of two linked lists
    intersect_node = intersectPoint(head1, head2);
    
      if(intersect_node == null) {
        System.out.println("No Intersection Point");
    }
    System.out.print("Intersection Point: " + intersect_node.data);
}
}

// This code is contributed by umadevi9616.
Python3 
# Python3 program to print intersection of lists

#  Link list node 
class Node:
    def __init__(self, data = 0, next = None):
        self.data = data
        self.next = next

# A utility function to return  intersection node
def intersectPoint(head1, head2):

    # Maintaining two pointers ptr1 and ptr2
    # at the head of A and B,
    ptr1 = head1
    ptr2 = head2

    # If any one of head is None i.e
    # no Intersection Point
    if (ptr1 == None or ptr2 == None):
        return None

    # Traverse through the lists until they
    # reach Intersection node
    while (ptr1 != ptr2):

        ptr1 = ptr1.next
        ptr2 = ptr2.next

      # If at any node ptr1 meets ptr2, then it is
      # intersection node.Return intersection node.
        if (ptr1 == ptr2):
            return ptr1

        # Once both of them go through reassigning,
        # they will be equidistant from the collision point.

        # When ptr1 reaches the end of a list, then
        # reassign it to the head2.
        if (ptr1 == None):
            ptr1 = head2

        # When ptr2 reaches the end of a list, then
        # redirect it to the head1.
        if (ptr2 == None):
            ptr2 = head1

    return ptr1

# Driver code

# Create two linked lists

# 1st Linked list is 3->6->9->15->30
# 2nd Linked list is 10->15->30

# 15 30 are elements in the intersection list

head1 = Node()
head1.data = 10
head2 = Node()
head2.data = 3
newNode = Node()
newNode.data = 6
head2.next = newNode
newNode = Node()
newNode.data = 9
head2.next.next = newNode
newNode = Node()
newNode.data = 15
head1.next = newNode
head2.next.next.next = newNode
newNode = Node()
newNode.data = 30
head1.next.next = newNode
head1.next.next.next = None
intersect_node = None

  # Find the intersection node of two linked lists
intersect_node = intersectPoint(head1, head2)

print("Intersection Point =", intersect_node.data)

# This code is contributed by shinjanpatra
C# 
// C# program to print intersection of lists
using System;
public class GFG {

    /* Link list node */
    public class Node {
        public int data;
        public Node next;
          public Node(int x) {
            data = x;
              next = null;
        }
    };

    // A utility function to return intersection node
    static Node intersectPoint(Node head1, Node head2)
    {

        // Maintaining two pointers ptr1 and ptr2
        // at the head of A and B,
        Node ptr1 = head1;
        Node ptr2 = head2;

        // If any one of head is null i.e
        // no Intersection Point
        if (ptr1 == null || ptr2 == null) {

            return null;
        }

        // Traverse through the lists until they
        // reach Intersection node
        while (ptr1 != ptr2) {

            ptr1 = ptr1.next;
            ptr2 = ptr2.next;

            // If at any node ptr1 meets ptr2, then it is
            // intersection node.Return intersection node.

            if (ptr1 == ptr2) {

                return ptr1;
            }
            /*
             * Once both of them go through reassigning,
             * they will be equidistant from the collision
             * point.
             */

            // When ptr1 reaches the end of a list, then
            // reassign it to the head2.
            if (ptr1 == null) {

                ptr1 = head2;
            }
            // When ptr2 reaches the end of a list, then
            // redirect it to the head1.
            if (ptr2 == null) {

                ptr2 = head1;
            }
        }

        return ptr1;
    }

    // Driver code
    public static void Main(String[] args)
    {

        /*
         * Create two linked lists
         *
         * 1st Linked list is 3.6.9.15.30 2nd Linked list
         * is 10.15.30
         *
         * 15 30 are elements in the intersection list
         */

        Node newNode;
        Node head1 = new Node(10);
        Node head2 = new Node(3);
        newNode = new Node(6);
        head2.next = newNode;
        newNode = new Node(9);
        head2.next.next = newNode;
        newNode = new Node(15);
        head1.next = newNode;
        head2.next.next.next = newNode;
        newNode = new Node(30);
        head1.next.next = newNode;
        head1.next.next.next = null;
        Node intersect_node = null;

        // Find the intersection node of two linked lists
        intersect_node = intersectPoint(head1, head2);

        if (intersect_node == null)
            Console.Write("No Intersection Point");
        else
            Console.Write("Intersection Point = "
                          + intersect_node.data);
    }
}

// This code is contributed by gauravrajput1
Javascript 
<script>
// Javascript program to print intersection of lists




/* Link list node */
class Node {
    constructor(x) {
        this.data = x;
        this.next = null;
    }
};

// A utility function to return  intersection node
function intersectPoint(head1, head2) {
    // Maintaining two pointers ptr1 and ptr2
    // at the head of A and B,
    let ptr1 = head1;
    let ptr2 = head2;

    // If any one of head is null i.e
    // no Intersection Point
    if (ptr1 == null || ptr2 == null) {

        return null;
    }

    // Traverse through the lists until they
    // reach Intersection node
    while (ptr1 != ptr2) {

        ptr1 = ptr1.next;
        ptr2 = ptr2.next;

        // If at any node ptr1 meets ptr2, then it is
        // intersection node.Return intersection node.

        if (ptr1 == ptr2) {

            return ptr1;
        }
        /* Once both of them go through reassigning,
        they will be equidistant from the collision point.*/

        // When ptr1 reaches the end of a list, then
        // reassign it to the head2.
        if (ptr1 == null) {

            ptr1 = head2;
        }
        // When ptr2 reaches the end of a list, then
        // redirect it to the head1.
        if (ptr2 == null) {

            ptr2 = head1;
        }
    }

    return ptr1;
}

// Driver code
/*
Create two linked lists

1st Linked list is 3.6.9.15.30
2nd Linked list is 10.15.30

15 30 are elements in the intersection list
*/

let newNode;
let head1 = new Node(10);
let head2 = new Node(3);
newNode = new Node(6);
head2.next = newNode;
newNode = new Node(9);
head2.next.next = newNode;
newNode = new Node(15);
head1.next = newNode;
head2.next.next.next = newNode;
newNode = new Node(30);
head1.next.next = newNode;
head1.next.next.next = null;
let intersect_node = null;

// Find the intersection node of two linked lists
intersect_node = intersectPoint(head1, head2);

if(intersect_node == null)
document.write("No Intersection Point");
else
document.write("Intersection Point = " + intersect_node.data);

// This code is contributed by Saurabh Jaiswal
</script>

Output
Intersection Point = 15

Time complexity : O( m + n ) 
Auxiliary Space:  O(1)

Find the intersection point by making a loop in the first list:

In this algorithm, we make the first list circular by connecting the last node to the first node. Then we take the size of the loop and move the first pointer in the second linked list by that number of nodes. Then take another pointer from the beginning of the second list and increment first and second pointer simultaneously to find the intersection point.

Steps to solve the problem:

  • Traverse the first linked list (count the elements) and make a circular linked list. (Remember the last node so that we can break the circle later on). 
  • Now view the problem as finding the loop in the second linked list. So the problem is solved. 
  • Since we already know the length of the loop (size of the first linked list) we can traverse those many numbers of nodes in the second list, and then start another pointer from the beginning of the second list. we have to traverse until they are equal, and that is the required intersection point. 
  • Remove the circle from the linked list. 

Please write comments if you find any bug in the above algorithm or a better way to solve the same problem.

Example :

C++ 
#include <iostream>

using namespace std;
// Node structure for singly linked list
struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};
// Function to find the intersection point of the two linked lists
ListNode *GFG(ListNode *headA, ListNode *headB) {
    if (!headA || !headB) return nullptr;
    // Make the first list circular by connecting the last node to the first node
    ListNode *curr = headA;
    while (curr->next) {
        curr = curr->next;
    }
    curr->next = headA;
    // Find the size of the loop.
    int size = 1;
    ListNode *temp = headA->next;
    while (temp != headA) {
        size++;
        temp = temp->next;
    }
    // Traverse the second linked list to the find the intersection point
    ListNode *slow = headB, *fast = headB;
    while (size--) {
        fast = fast->next;
    }
    while (slow != fast) {
        slow = slow->next;
        fast = fast->next;
    }
    // Remove the circle from the linked list
    curr->next = nullptr;
    return slow; // Return the intersection point
}
int main() {
    // Example linked lists
    ListNode *headA = new ListNode(4);
    headA->next = new ListNode(1);
    headA->next->next = new ListNode(8);
    headA->next->next->next = new ListNode(4);
    headA->next->next->next->next = new ListNode(5);
    ListNode *headB = new ListNode(5);
    headB->next = new ListNode(0);
    headB->next->next = new ListNode(1);
    headB->next->next->next = headA->next->next;
    // Find the intersection point
    ListNode *intersection = GFG(headA, headB);
    if (intersection)
        cout << "Intersection point value: " << intersection->val << endl;
    else
        cout << "No intersection point found." << endl;
    return 0;
}
Python3 
# Node structure for singly linked list
class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

# Function to find the intersection point of the two linked lists
def get_intersection(headA, headB):
    if not headA or not headB:
        return None

    # Make the first list circular by connecting the last node to the first node
    curr = headA
    while curr.next:
        curr = curr.next
    curr.next = headA

    # Find the size of the loop.
    size = 1
    temp = headA.next
    while temp != headA:
        size += 1
        temp = temp.next

    # Traverse the second linked list to find the intersection point
    slow = headB
    fast = headB
    for _ in range(size):
        fast = fast.next

    while slow != fast:
        slow = slow.next
        fast = fast.next

    # Remove the circle from the linked list
    curr.next = None
    return slow  # Return the intersection point

# Example linked lists
headA = ListNode(4)
headA.next = ListNode(1)
headA.next.next = ListNode(8)
headA.next.next.next = ListNode(4)
headA.next.next.next.next = ListNode(5)

headB = ListNode(5)
headB.next = ListNode(0)
headB.next.next = ListNode(1)
headB.next.next.next = headA.next.next

# Find the intersection point
intersection = get_intersection(headA, headB)
if intersection:
    print("Intersection point value:", intersection.val)
else:
    print("No intersection point found.")

output :

Intersection point value: 8


Like Article
Suggest improvement
Previous
Modify contents of Linked List
Next
Circular Linked List Implementation of Circular Queue
Share your thoughts in the comments

Similar Reads

Find intersection point of two Linked Lists without finding the length
Python Program For Finding Intersection Point Of Two Linked Lists
C++ Program For Finding Intersection Point Of Two Linked Lists
C Program For Finding Intersection Point Of Two Linked Lists
Java Program For Finding Intersection Point Of Two Linked Lists
C# Program For Finding Intersection Point Of Two Linked Lists
Javascript Program For Finding Intersection Point Of Two Linked Lists
Get the Intersection point of two Linked List by counting nodes
Intersection point of two Linked List by marking visited nodes
C++ Program For Finding Intersection Of Two Sorted Linked Lists
https://media.geeksforgeeks.org/auth/avatar.png
GeeksforGeeks
Article Tags :
Practice Tags :
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox